一. 基本概念1. 概念及定义数据(Data)数据元素数据对象数据结构2. 四种逻辑结构3. 四种基本存储结构顺序存储结构链式存储结构索引存储结构散列存储结构4. 数据类型、抽象数据类型4.1 数据类型4.2 抽象数据类型(ADT)二. 算法1. 算法基本概念2. 算法效率度量2.1 时间复杂度2.2 空间复杂度三. 线性表1. 线性表定义2. 线性表的基本操作3. 顺序表3.1 顺序表的静态分配3.2 顺序表的动态分配3.3 顺序表的插入3.4 顺序表的删除3.5 顺序表的查找4. 单链表4.1 单链表建立4.1.1 尾插法4.1.2 头插法建立链表4.2 单链表的插入4.3 单链表的删除4.4 链表的查找4.5 习题:链表的逆置5. 双链表5.1 双链表的初始化5.2 双链表的插入5.3 双链表的删除6. 循环链表6.1 循环单链表的初始化6.2 循环双链表的初始化7. 静态链表7.1 静态链表的初始化8. 顺序表和链表的比较四. 栈1. 栈的顺序存储实现1.1 栈的定义1.2 栈的增加1.3 出栈操作1.4 共享栈2. 链栈2.1 链栈初始化2.2 链栈的入栈2.3 链栈的出栈2.4 链栈打印3. 栈的应用—括号匹配4. 栈的应用—表达式求值4.1 中缀表达式转后缀方法4.2 后缀表达式计算4.3 代码实现5. 栈在递归中的应用五. 队列1. 队列的顺序实现1.1 队列初始化1.2 入列1.3 出列1.4 队列元素个数1.5 其他情况2. 链式队列2.1 链式队列的初始化2.2 链式队列的入队2.3 链式队列出队操作3. 双端队列4. 队列的应用——树的遍历5. 特殊矩阵的压缩存储5.1 一维数组5.2 二维数组5.3 对称矩阵压缩存储5.4 三角矩阵5.5 三对角矩阵的压缩存储5.6 稀疏矩阵压缩存储六. 串1. 串的存储方法2. 串的顺序存储2.1 定长顺序存储2.2 堆分配存储3. 串的链式存储3.1 低密度存储3.2 高密度存储4. 字符串基本操作4.1 求字串4.2 字符串比较4.3 定位操作5. 朴素模式匹配算法6. KMP算法匹配字符串7. 求next数组8. KMP算法进一步优化七 树1. 树的基本概念2. 树常考的性质3. 二叉树3.1 几个特殊二叉树满二叉树完全二叉树二叉排序树平衡二叉树3.2 二叉树存顺序储结构完全二叉树顺序存储非完全二叉树顺序存储3.3 二叉树的链式存储3.4 二叉树遍历三种遍历方法二叉树层序遍历3.5 通过遍历序列构造二叉树3.6 线索二叉树线索二叉树概念线索二叉树代码实现线索二叉树找前驱与后继4. 树的存储与遍历4.1 树与森林的存储方法双亲表示法孩子表示法孩子兄弟表示法森林转换二叉树二叉树转换为森林4.2 树和森林的遍历先根遍历树的后根遍历(深度优先遍历)树的层次遍历(广度优先遍历)森林的先序遍历森林的中序遍历5. 哈夫曼树5.1 哈夫曼树的构造5.2 哈夫曼树的应用八. 并查集1. 集合查操作2. 集合的合并操作3. 并查集的优化4. 并查集优化2
一. 基本概念
数据结构三要素:逻辑结构、数据的运算、物理结构(存储结构)
提取操作对象,找出操作对象之间的关系并用数学的语言描述就是数据结构。
操作对象指:每位学生的信息(学号、姓名、性别.....)
操作的算法指:查询、插入、修改、删除等。
数据结构可分为:线性数据结构(数组,队列,线性表等)、非线性数据结构(集合,树,图等)。
线性数据结构:有且仅有一个开始和一个终端结点,并且所有结点都最多只有一个直接前趋和一个直接后继。如:学生管理系统,是一对一关系
非线性数据结构:一个结点可能油多个直接前趋和直接后继。如:目录结构(树)、最短路径(图),是一对多关系或多对多关系。

1. 概念及定义
数据(Data)
数据是能输入计算机且能被计算机处理的各种符号的集合。
数据特点:
- 信息的载体
- 是对客观事物符号化的表示
- 能够被计算机识别存储和加工
数据包括:
- 数值型的数据:整数、实数等。
- 非数值型的数据:文字、图像、图形、声音等。
数据元素
数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。而一个数据元素可由多个数据项组成,数据项是构成数据元素不可分割最小单位。
也可称为元素,或称为记录、结点或顶点。如上面最短路径图,其中的每个点我们称之为结点。
数据项
数据项是构成元素的不可分割的最小单位。
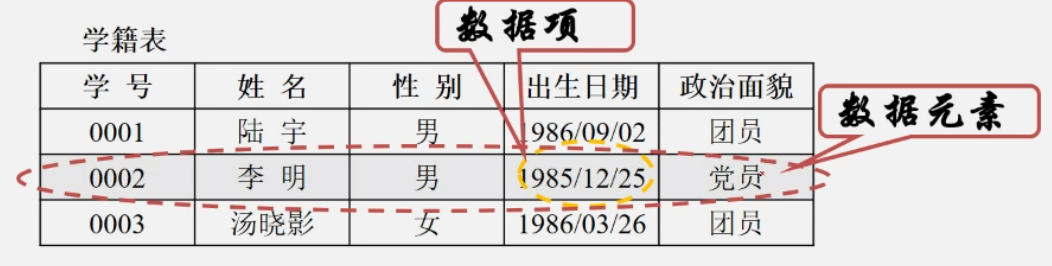
上面每行可称为数据元素,而每列可以称之为数据元素中的数据项。
三者关系
数据
例子:学生表
数据对象
数据对象是性质相同的数据元素的集合,是数据的一个子集。
如:学籍表可以看作是一个数据对象,由若干条学生信息构成的子集。
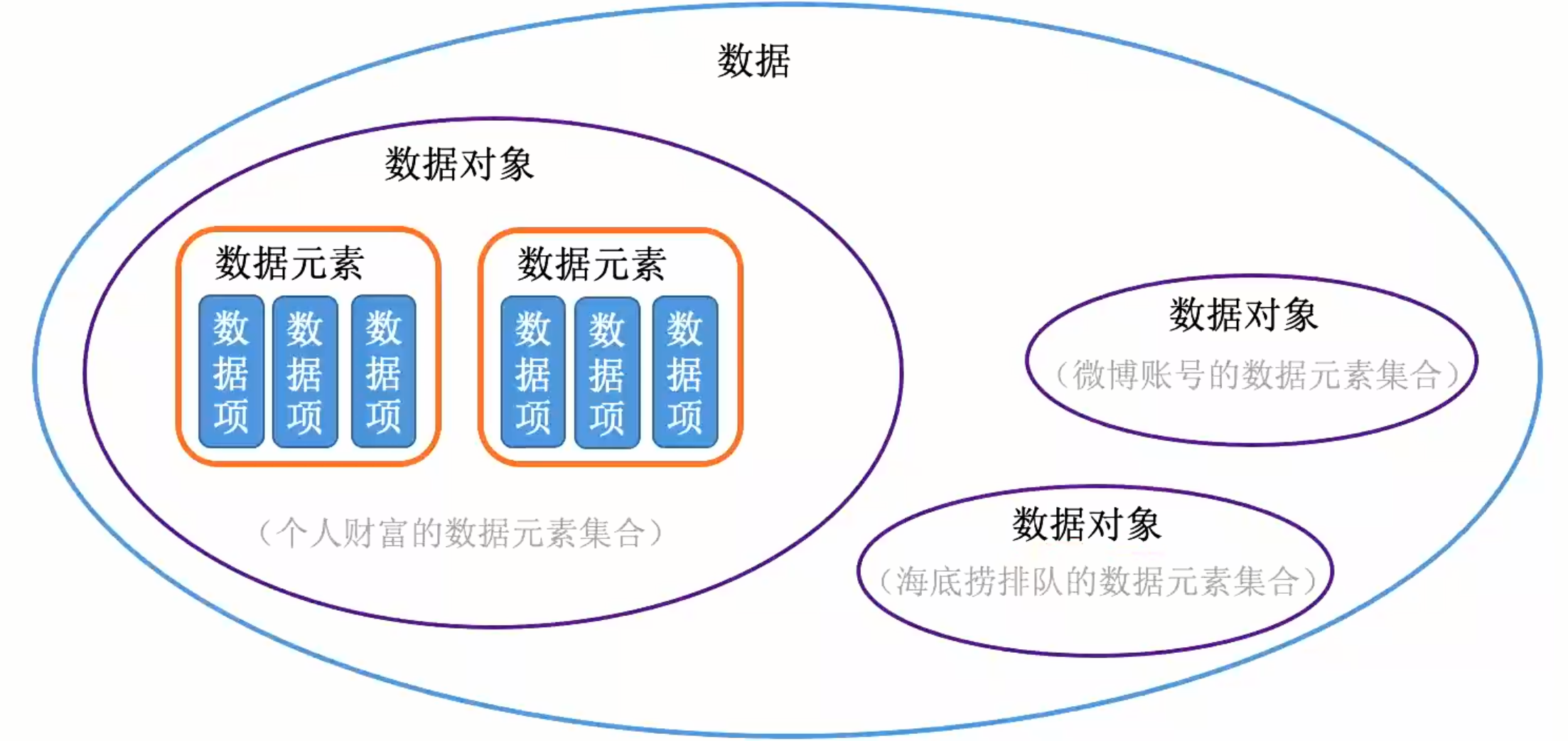
数据元素和数据对象关系
数据元素:组成数据的基本单位。其与数据的关系是:数据元素是集合的个体。
数据对象:性质相同的数据元素的集合。其与数据的关系是:集合的子集。
数据结构
意义:数据元素不是孤立存在的,它们之间存在着某种关系,数据元素相互之间的关系称为结构( Structure )
数据结构是指相互之间存在一种或多种特定关系的数据元素集合。或者说,数据结构是带结构的数据元素的集合。
数据结构包含内容:
- 数据元素之间的逻辑关系,也称为逻辑结构。
- 数据元素及其关系在计算机内存中的表示(又称为映像),称为数据的物理结构或数据的存储结构。
- 数据的运算和实现,即对数据元素可以施加的操作以及这些操作在相应的存储结构上的实现。
数据结构的两个层次
逻辑结构:
描述数据元素之间的逻辑关系
与数据存储无关,独立于计算机
是从具体问题抽象出来的数学模型
物理结构(存储结构):
数据元素及其关系在计算机存储器中的结构(存储方式)
是数据结构在计算机中的表示
逻辑结构和存储结构的关系:
存储结构是逻辑关系的映像与元素本身的映像。
逻辑结构是数据结构的抽象,存储结构是数据结构的实现。
两者综合起来建立了数据元素之间的结构关系。
2. 四种逻辑结构
逻辑结构和数据的运算是定义一种数据结构前提。
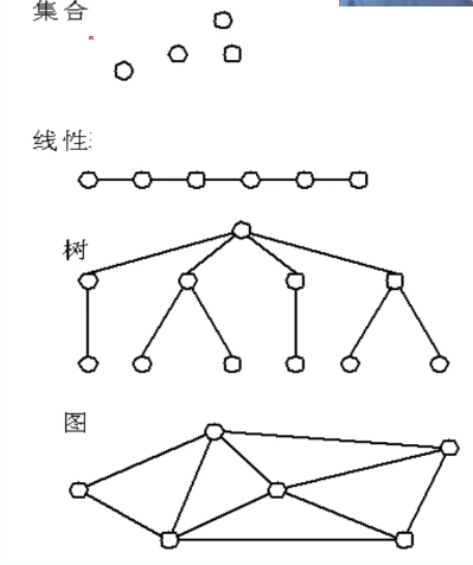
集合结构(大纲不考):结构中的数据元素之间除了同属于一个集合的关系外,无任何其它关系。
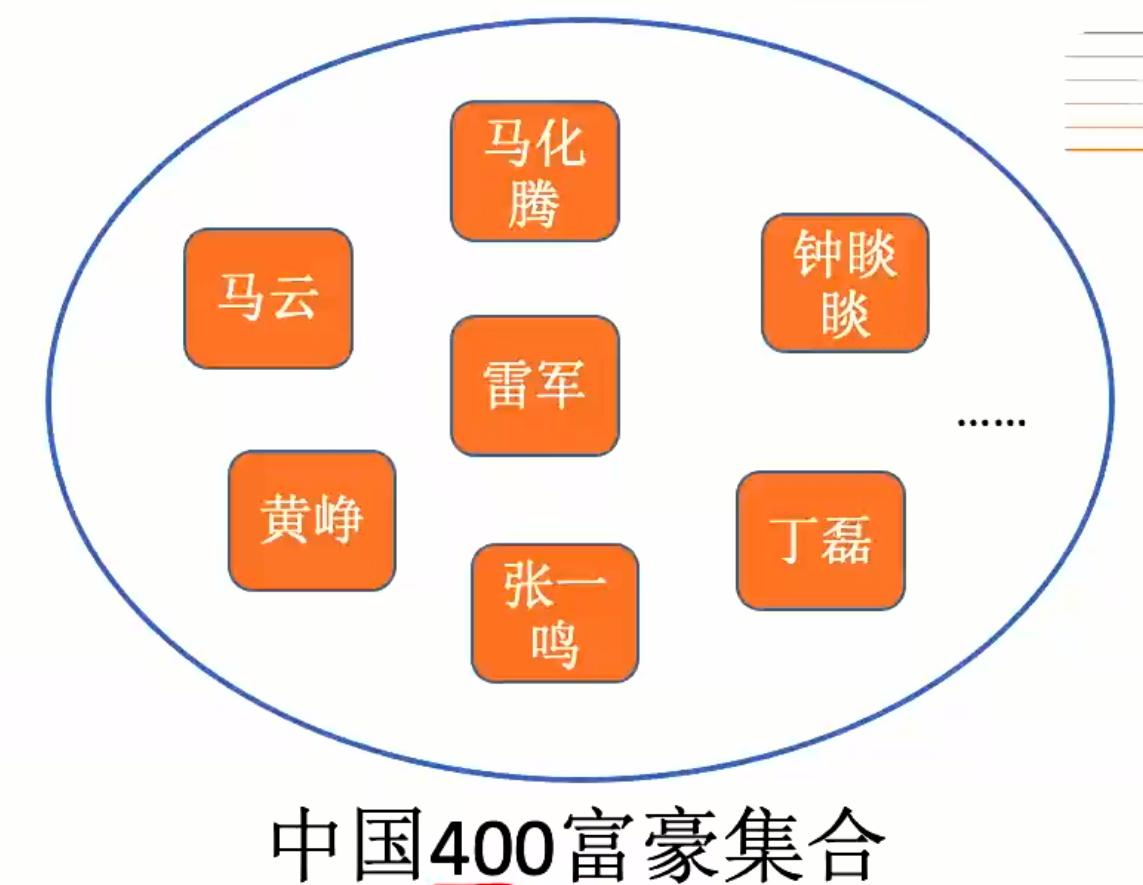
线性结构:结构中的数据元素之间存在着一对一的线性关系,除了除了第一个元素,所有元素都有唯一前驱;除了最后一个元素,所有元素都有唯一后继。
基本运算:①查找第
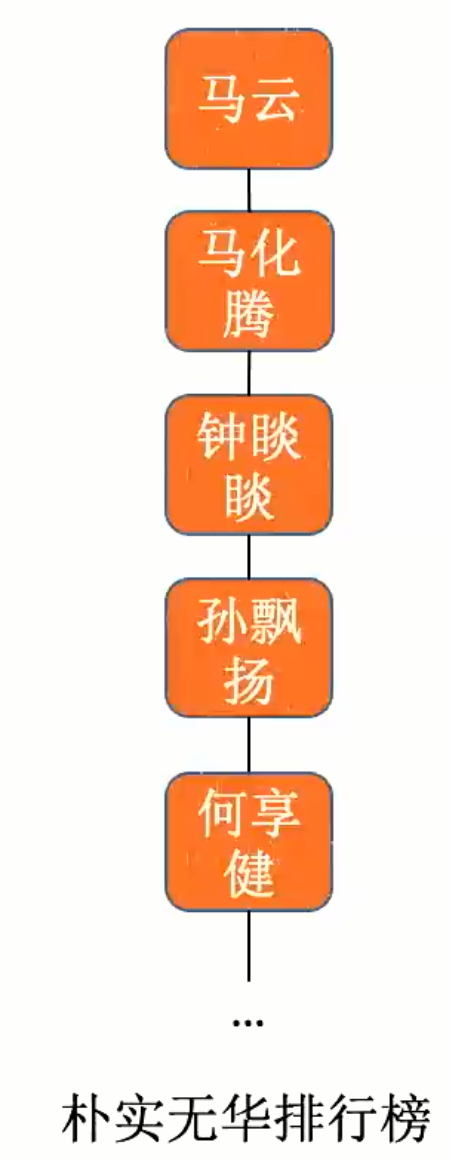
树形结构:结构中的数据元素之间存在着一对多的层次关系。
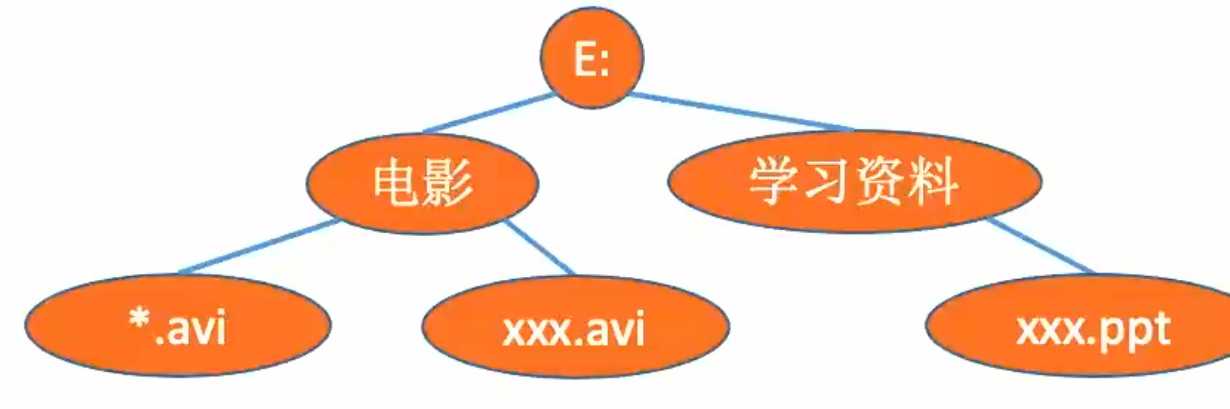
图状结构或网状结构:结构中的数据元素之间存在着多对多的任意关系。

3. 四种基本存储结构
当我们定义完一种数据结构后,需要用计算机来实现这种数据结构,此时用到基本存储结构。
顺序存储结构
含义:
- 用一组连续的存储单元依次存储数据元素,数据元素之间的逻辑关系由元素的存储位置来表示。
- C语言中用数组来实现顺序存储结构
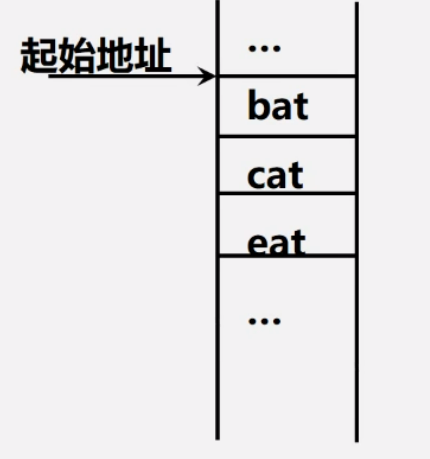
链式存储结构
含义:
- 用一组任意的存储单元存储数据元素,数据元素之间的逻辑关系用指针表示。
- C语言中用指针来实现链式存储结构。

如:上图
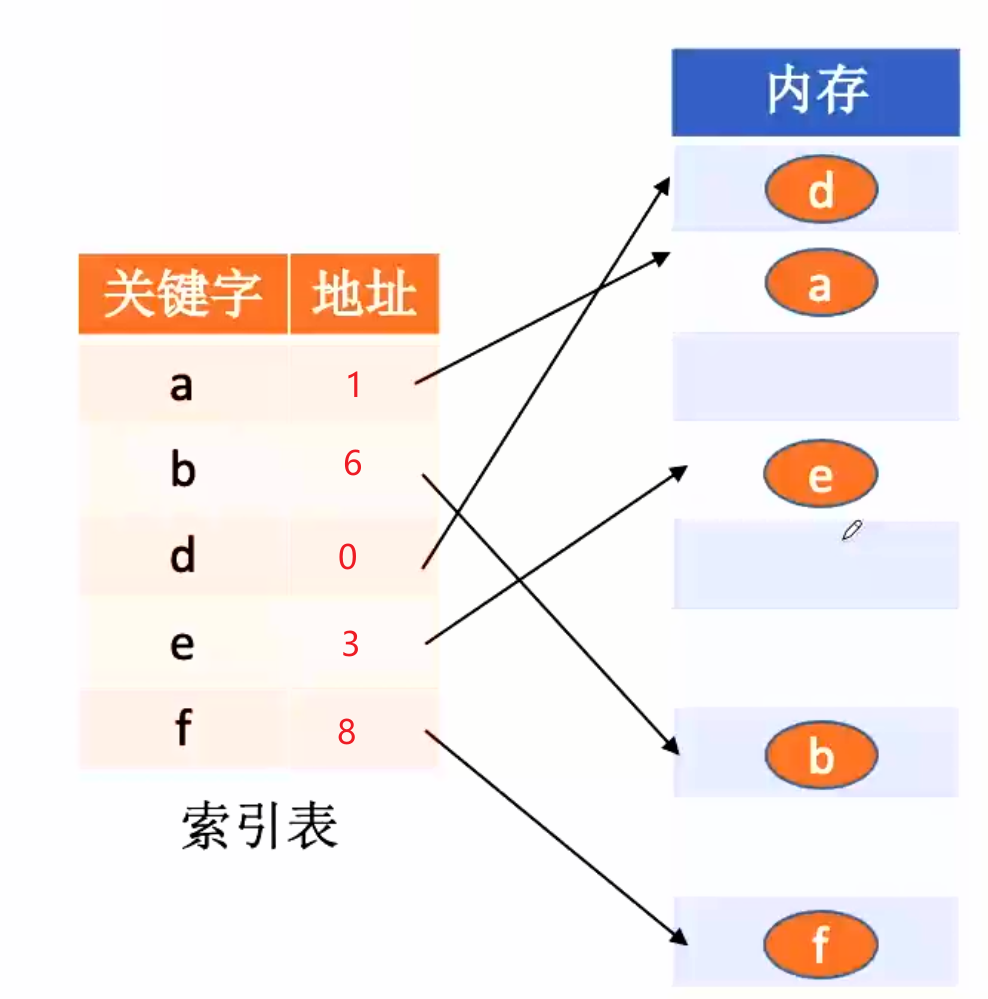
索引存储结构
含义:
- 在存储结点信息的同时,还建立附加的索引表。
- 通俗讲索引就是目录,一般形式是:关键字、地址。
- 关键字是能唯一标识一个结点的数据项。
- 若每个结点在索引表中都有一个索引项,则该索引表称之为稠密索引。若一组结点在索引表中只对应一个索引项,则该索引表称之为稀疏索引。
散列存储结构
根据结点的关键字直接计算出该结点的存储地址。如:哈希表。
4. 数据类型、抽象数据类型
4.1 数据类型
数据类型是一个值的取值范围和定义在此范围上的一组操作(加减、取模等)的总称。
- 原子类型:其值不可再分的数据类型。如
- 结构类型:其值可以再分解为若干成分(分量)的数据类型。如定义一个可操作横坐标和纵坐标的函数。
4.2 抽象数据类型(ADT)
抽象数据类型是抽象数据组织及与之相关的操作。如:逻辑结构、数据运算、物理结构(存储结构),这个过程。
二. 算法
1. 算法基本概念
算法就是如何高效地处理这些数据,以解决实际问题。
其定义是对特定问题求解步骤地一种描述,它是指令的有限序列,其中的每条指令表示一个或多个操作。
算法特点:
- 有穷性。一个算法必须总在执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性。算法中每条指令必须有确切的含义,对于相同的输入只能得出相同的输出。
- 可行性。算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
- 输入。 一个算法有零个或多个输入, 这些输入取自于某个特定的对象的集合。 输出。一个算法有一个或多个输出,这些输出是与输入有着某种特定关系的量。
以上特点只要有一个不满足,就不能称之为算法。
一个好的算法所具备特质:
- 正确性。算法能够正确解决求解问题。
- 可读性。算法应具有良好的可读性,以帮助人们理解。考试时候要写注释。
- 健壮性。输入非法数据时,算法能适当地做出反应或进行处理,而不会产生莫名其妙的输出结果。
- 高效率和低存储。即算法时间复杂度低,空间复杂度低。

2. 算法效率度量
算法复杂度度量可以从两个方面:①时间复杂度、②空间复杂度
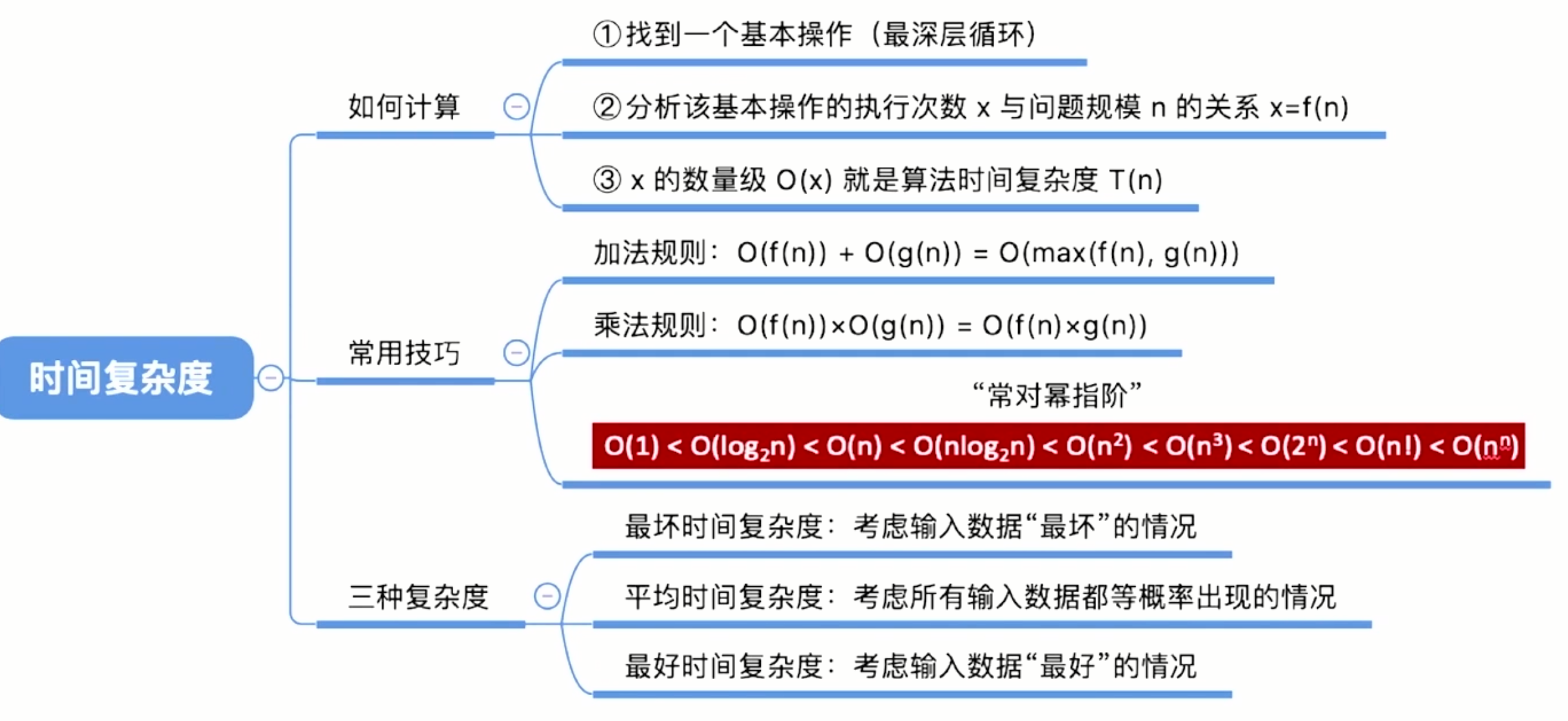
2.1 时间复杂度
用事前预估算法时间开销
与问题规模 的关系( 表示"time")。
方法:
时间复杂度加法规则:
我们可以通过对每一行有效代码进行时间记录,从而估计出代码所需的执行时间。如下:
1void loveYou(int n) { //n 为问题规模2int i=1;//爱你的程度3while(i<=n){4i++ ;5//每次+16printf("I Love You %d\n",i);7}8printf("I Love You More Than %d\n",n) ;9}10int main( ){11loveYou(3000) ;12}以上代码模拟打印3000遍I Love You。运行结果如下:
xxxxxxxxxx91....2I Love You 29943I Love You 29954I Love You 29965I Love You 29976I Love You 29987....8I Love You 30019I Love You More Than 3000我么可以估计一下语句执行时间:①⑤各执行一次,②执行3001次,③④执行3000次,所以变量
虽然我们通过如此简单方式得出这段程序所需执行时间,但是广义化之后该方法并不适用:如果代码是几万行的这种方法显然不适用。
根据我们所学数学知识,我们想得到一个估计大小时,一个表达式中更低阶部分我们往往可以省略。所以上面可以写为
我们一般用
结论:一个程序的算法复杂度可以只考虑阶数高的部分。以上是时间复杂度计算的加法规则,同样我们可以推出以下的规则:
乘法规则
即多项相乘,都保留。如:
混合运算规则
混合运算需要保留最大那个项。为了方便理解我们可以保留其中变化趋势最大函数,函数变化趋势如下:

例子:
通过以上规则我们还要注意以下几点:
- 顺序执行的代码只会影响常数项,所以可以忽略不记。
- 循环执行代码中,我们只需要挑一个循环体基本操作,分析他的执行次数即可。
- 如果有多层嵌套循环,我们只需要关注最深层代码循环次数即可。
例1:分析以下代码时间复杂度
xxxxxxxxxx91//算法3- 指数递增型爱 你2void loveYou(int n) { //n 为问题规模3 int i=1;//爱你的程度4 while(i<=n){5 i=i*2; //每次翻倍6 printf("I Love You %d\n",i); 7 }8 printf("I Love You More Than %d\n",n);9}答案:
解析:我们直接看循环体,循环体中,赋值语句
每次翻倍,假设循环了 次,则循环结束时刚好满足 ,所以 则,时间复杂度
例2:分析以下代码时间复杂度
xxxxxxxxxx151void loveYou(int flag[], int n) { //n 为问题规模2 printf("I Am Iron Man\n") ;3 for(int i=0; i<n; i++){ //从第一个元素开始查找4 if(flag[i]==n){ //找到元素n5 printf("I Love You %d\n",n) ;6 break; //找 到后立即跳出循环7 }8 }9}10//其中flag数组是1~n个数,输入一个数n找出n在数组中的位置11int main(){12 int flag[n]={1...n};13 loveYou(flag,n); 14 return 0;15}答案:最好情况:元素n在第一个位置,即最好时间复杂度
最坏情况:元素n在最后一个位置,最坏时间复杂度 平均情况:假设元素n在任意一个位置的概率相同为 ,平均时间复杂度 平均情况解析:循环次数
,即
注意:我们在评价一个算法时候一般只看最坏情况和平均情况,而最好情况一般参考意义不大。
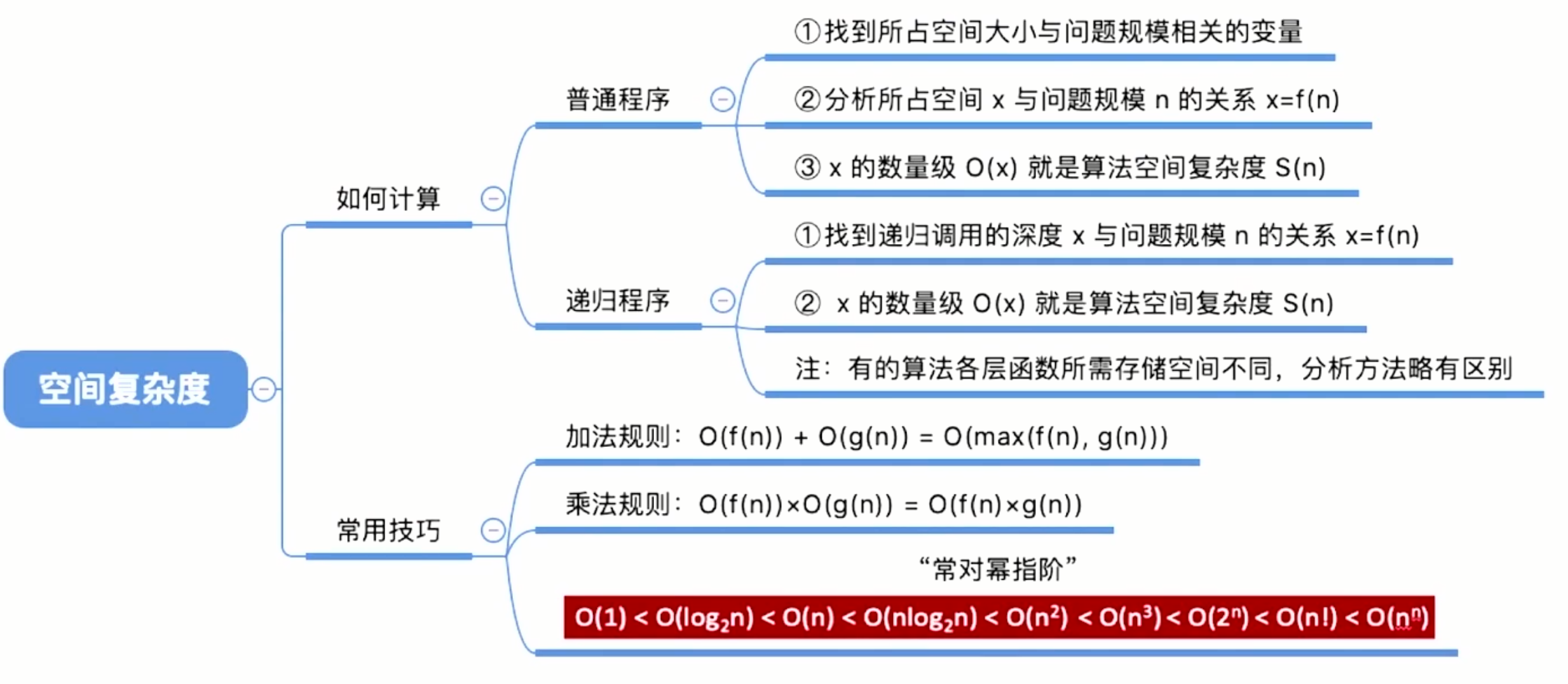
2.2 空间复杂度
空间复杂度需要时间复杂度中运算知识。空间复杂度我们用
例1:计算以下程序空间复杂度
xxxxxxxxxx61void test(int n) {2 int flag[n];3 //声明一个长度为n的数组4 int i;5 //.....此处省略很多代码6}答案:
解析:函数所需要参数
占四个字节,下面的 类型所以也是四字节,数组长度是 且为int类型,所以是 ,那么这个程序所需要空间为: 。规范写法为
结论:常数项同样不考虑,注意数组大小等。
例2:计算以下程序空间复杂度
xxxxxxxxxx71void test(int n) {2 int flag[n][n]; //声明 n*n的二维数组3 int otheg[n];4 //声明一个长度为n的数乡5 int i;6 //.... .此处省略很多代码7}答案:
解析:二维int类型n长度数组占大小为:
,下面一维数组是 ,所以
例3:计算以下程序空间复杂度
xxxxxxxxxx111void loveYou(int n) { //n 为问题规模2 int a,b,c; //声明一 系列局部变量3 //...省略代码4 if(n>1){5 loveYou(n-1);6 }7 printf("I Love You %d\n", n);8}9int main(){10 loveYou(n)11}答案:
解析:函数递归
次,每次变量大小占 ,所以应该为
结论:递归问题空间复杂
例4:我们对例3进行改进,讲声明变量改为数组
xxxxxxxxxx111void loveYou(int n) { //n 为问题规模2 int flag[n]; //声明一 系列局部变量3 //...省略代码4 if(n>1){5 loveYou(n-1);6 }7 printf("I Love You %d\n", n);8}9int main(){10 loveYou(n)11}答案:
解析:函数递归调用
次,每次数组长度为 ,所以空间复杂度为: ,即答案。
三. 线性表
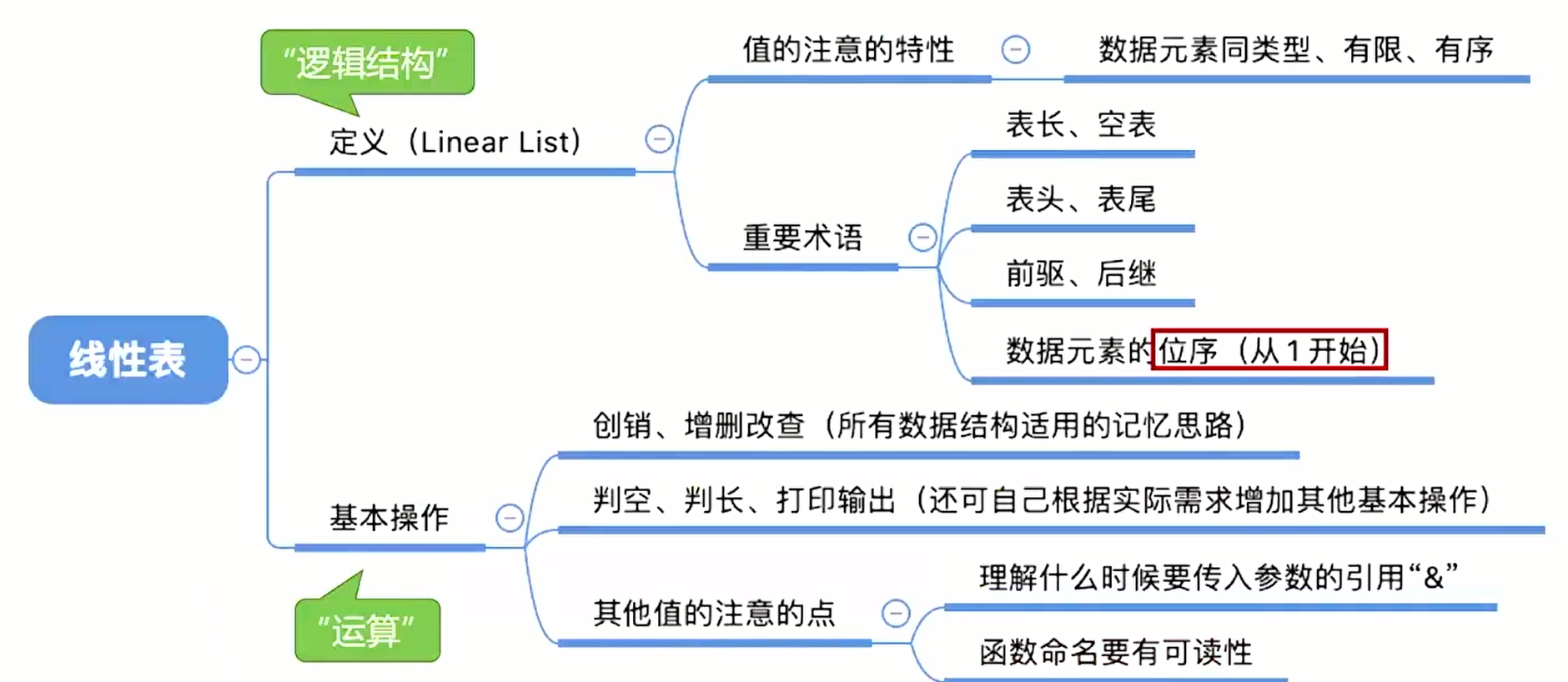
1. 线性表定义
定义:线性表是具有相同数据类型的
几个概念:
- 除第一个元素外,每个元素有且仅有一个直接前驱;除最后一个元素外,每个元素有且仅有一个直接后继。
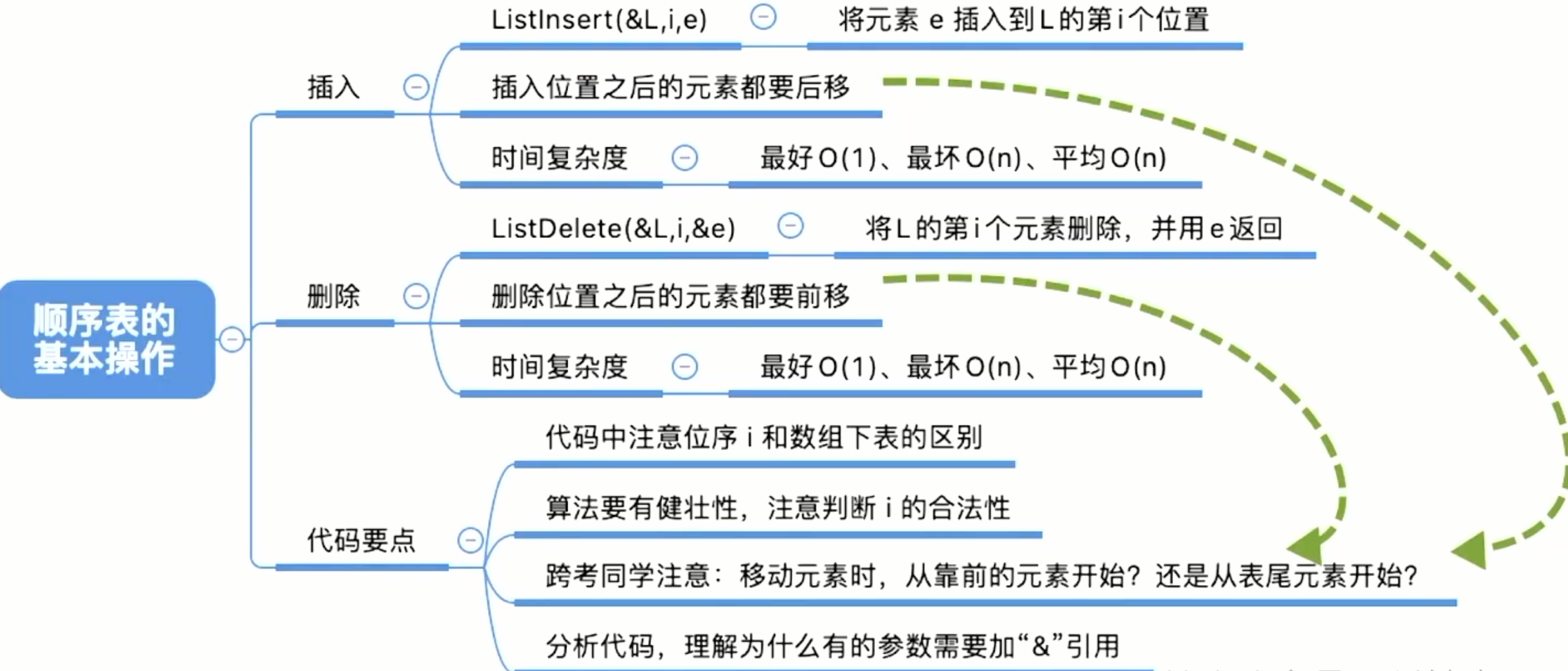
2. 线性表的基本操作
InitList(&L):初始化表。构造一个空的线性表
ListInsert(&L,i,e):插入操作。在表
LocateElem(L,e):按值查找操作。在表
其他常用操作: Length(L):求表长。返回线性表L的长度,即L中数据元素的个数。 PrintList(L):输出操作。按前后顺序输出线性表L的所有元素值。 Empty(L):判空操作。若L为空表,则返回true,否则返回false。
以上括号内的是参数。
总结:
对数据的操作:创建,销毁、增删改查
函数名和参数的形式、命名都可改变。对于命名一般用驼峰命名法:
方法名、参数名、成员变量、局部变量需要使用小驼峰命名法
类名需要使用大驼峰命名法
什么时候要传入引用"&":对参数的修改结果需要"带回来"。解释如下:
xxxxxxxxxx1112void test(int & x) {3x=1024;4printf( "test函数内部x=%d\n",x);5}6int main() {7int X=1;8printf("调用test前x=%d\n",x) ;9test(X) ;10printf( "调用test后x=%d\n",x) ;11}运行结果:
调用test前x=1 test函数内部x=1024 调用test后x= 1024
这里test函数中的
3. 顺序表
顺序表是线性表的一种。其定义是:用顺序存储的方式实现线性表顺序存储。把逻辑上相邻的元素存储在物理位置,上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
顺序表优缺点:
- 优点:可随机存取,存储密度高
- 缺点:要求大片连续空间,改变容量不方便
我们可以用

3.1 顺序表的静态分配
xxxxxxxxxx51//定义最大长度2typedef struct{3 ElemType data[MaxSize]; //用静态的“数组”存放数据元素4 int length; //顺序表的当前长度5}SqList; //顺序表的类型定义(静态分配方式)给各个数据元素分配连续的存储空间,大小为
。即数组大小 数据类型。 注意:
语言要初始化数据。否则会出现"脏数据"情况。
静态分配存在一定局限性:无法提前预知数组大小。
3.2 顺序表的动态分配
malloc(动态申请空间):SeqList.data = (ElemType *) malloc (sizeof(ElemType) * InitSize);
malloc函数返回一个指针,需要强制转型为你定义的数据元素类型指针。
free(删除申请空间):free(SeqList.data)
xxxxxxxxxx61//顺序表的初始长度2typedef struct{3 ElemType *data; //指示动态分配数组的指针4 int MaxSize; //顺序表的最大容量5 int length; //顺序表的当前长度6} SeqList; //顺序表的类型定义(动态分配方式)动态分配案例:
x1using namespace std;3struct stu{4 int *arr;5 int len;6};7void initArr(stu &l){ //初始化arr指针,并未其分配初始空间8 int i=0,j=0;9 l.arr=(int *)malloc(10*sizeof(int));10 l.len=0;11 while(cin>>i){ //输入数组值12 l.arr[j]=i;13 l.len++;14 j++;15 }16}17
18void insertArr(stu &l,int cout){ //扩大arr指针空间19 int *p=l.arr;20 l.arr=(int *)malloc((cout+l.MaxSize)*sizeof(int));21 for(int i=0;i<l.len;i++){22 l.arr[i]=p[i];23 printf("指针值:%d\n",p[i]);24 }25 free(p);26}27int main(){28 stu l;29 initArr(l);30 insertArr(l,3);31 for(int i=0;i<l.len;i++){32 cout<<l.arr[i]<<endl; //输出扩大后的数组arr33 }34} 顺序表的特点:
- 随机访问,即可以在
- 存储密度高,每个节点存储数据元累
- 拓展容量不方便(即便采用动态分配的方式实现,拓展长度的时间复杂度也比较高)
- 插入、删除操作不方便,需要移动大量元素
3.3 顺序表的插入
xxxxxxxxxx231//定义最大长度2typedef struct{3 int data[MaxSize]; //用静态的"数组"存放数据4 int length; //顺序表的当前长度5}SqList; //顺序表的类型定义6bool ListInsert(SqList &L,int i,int e){7 if(i<1||i>L.length+1) //判断i的范围是否有效8 return false;9 if(L.length>=MaxSize) //当前存储空间已满,不能插入10 return false;11 for(int j=L.length;j>=i;j--)//将第1个元素 及之后的元素后移12 L.data[j]=L.data[j-1];13 L.data[i-1]=e; //在位置i处放入e 14 L.length++; //长度加115 return true ;16}17int main( ) {18 SqList L; //声明一个顺序表19 InitList(L); //初始化顺序表20 //...此处省略一些代码,插入几个元素21 ListInsert(L,3,3);22 return 0;23}以上就是对顺序表进行元素插入操作。
我们可以对以上ListInsert()方法进行时间复杂度分析:
最好情况:新元素插入到表尾,不需要移动元素。
最坏情况:新元素插入到表头,需要将原有的
平均情况:假设新元素插入到任何一个位置的概率相同,即
当
所以平均循环次数
由此可得时间复杂度为
3.4 顺序表的删除
xxxxxxxxxx251//定义最大长度2typedef struct{3 int data[MaxSize]; //用静态的"数组"存放数据4 int length; //顺序表的当前长度5}SqList; 6bool ListDelete(SqList &L,int i,int &e){7 if(i<1||i>L.length) //判断i的范围是否有效8 return false;9 e=L.data[i-1]; //将被删除的元素赋值给e10 for(int j=i;j<L.length;j++) //将第i个位 置后的元素前移11 L.data[j-1]=L.data[j];12 L.length--; //线性表长度减113 return true ;14}15int main() {16 SqList L; //声明一个顺序表17 InitList(L); //初始化顺序表18 //.. .此处省略一些代码,插入几个元素19 int e; //用变量e把删除的元素”带回来”20 if (ListDelete(L,3,e))21 printf("已删除第3个元素,删除元素值为=%d\n",e);22 else23 printf("位序i不合法,删除失败\n");24 return 0;25}运行结果:已删除第3个元素,删除元素值为
我们可以对以上ListDelete()方法进行时间复杂度分析:
最好情况:删除表尾元素,不需要移动其他元素
最坏情况:删除表头元素,需要将后续的
平均情况:假设删除任何一个元素的概率相同,即
平均循环次数为
由此可得时间复杂度为
3.5 顺序表的查找
按位查找
获取表L中第i个位置的元素的值。静态分配方式:
xxxxxxxxxx912//定义最大长度3typedef struct{4ElemType data [MaxSize];//用静态的“数组”存放数据元素5int length; //顺序表的当前长度6}SqList; //顺序表的类型定义(静态分配方式)7ElemType GetElem(SqList L,int i){8return L.data[i-1];9}动态分配方式:
xxxxxxxxxx91//顺序表的初始长度2typedef struct{3ElemType *data; //指示动态分配数组的指针4int MaxSize; //顺序表的最大容量5int length; //顺序表的当前长度6} SeqList; //顺序表的类型定义(动态分配方式)7ElemType GetElem(SqList L,int i){8return L.data[i-1];9}由于顺序表的各个数据元素在内存中连续存放,因此可以根据起始地址和数据元素大小立即找到第
按值查找
注意:不能直接判断两个结构体是否相等。如果要判断我们需要对结构体一个一个比较。
基本数据类型如:int、 char、 double、float等可以直接用运算符"=="比较。但
xxxxxxxxxx131//顺序表的初始长度2typedef struct{3ElemType *data; //指示动态分配数组的指针4int MaxSize; //顺序表的最大容量5int length; //顺序表的当前长度6} SeqList; //顺序表的类型定义(动态分配方式)7//在顺序表L中查找第一一个元素值等于e的元素,并返回其位序8int LocateElem(SeqList L,ElemType e){9for(int i=0;i<L. length; i++)10if(L.data[i]==e)11return i+1; // 数组下标为i的元素值等于e,返回其位序i+112return 0; //退出循环,说明查找失败13}该算法的时间复杂度:
最好情况:目标元素在表头,循环
最坏情况:目标元素在表尾,循环
平均情况:假设目标元素出现在任何一个位置的概率相同, 都是
目标元素在第
平均循环次数:
即时间复杂度为

4. 单链表
链表不同于顺序表的顺序存储方式,用的是链式存储。
单链表的每个结点除了存放数据元素,同时还需要包含指向下一个结点的指针。由于每个结点只包含一个指针所以叫单链表。
单链表优缺点:
- 优点:不要求大片连续空间,改变容量方便
- 缺点:不可随机存取,要耗费一定空间存放指针,无法逆向检索。
单链表定义如下:
xxxxxxxxxx41struct LNode{2 ElemType data;3 struct LNode *next;4}上面的"LNode"称之为结点,data称为数据域,*next称为指针域。
带头节点的单链表:
xxxxxxxxxx191typedef struct LNode{2 int data; //定义单链表结点类型3 struct LNode *next; //每个节点存放一个数据元素4}LNode,*LinkList; //指针指向下一个节点5
6//初始化一个空的单链表7bool InitList(LinkList &L) {8 L = (LNode *)malloc(sizeof(LNode)); //分配一个头结点9 if (L==NULL) //内存不足,分配失败10 return false;11 L->next = NULL; //头结点之后暂时还没有节点12 return true;13}14void test(){15 LinkList L; //声明一个指向单链表的指针16 //初始化一个空表17 InitList(L);18 //......后续代码......19}上面前四行代码是将"struct LNode"命名为"LNode",并且用"LinkList"表示一个指向"struct LNode"的指针。
不带头结点单链表
xxxxxxxxxx161typedef struct LNode{2 int data; //定义单链表结点类型3 struct LNode *next; //每个节点存放一个数据元素4}LNode,*LinkList; //指针指向下一个节点5
6//初始化一个空的单链表7bool InitList(LinkList &L) {8 L = NULL; //空表,暂时还没有任何结点9 return true;10}11void test(){12 LinkList L; //声明一个指向单链表的指针13 //初始化一个空表14 InitList(L);15 //......后续代码......16}4.1 单链表建立
4.1.1 尾插法
先初始化一个带头结点的单列表,之后每次取个数据元素插入表尾部。是比较常用的方法。
先初始化链表:
xxxxxxxxxx131typedef struct LNode{2int data; //定义单链表结点类型3struct LNode *next; //每个节点存放一个数据元素4}lNode,*linkList; //指针指向下一个节点56//初始化链表7bool initList(linkList &l){8l=(lNode*)malloc(sizeof(lNode)); //链表开辟一个头节点9if(l==NULL)10return false;11l->next=NULL; //头结点指针域指向空12return true;13}创建链表:
xxxxxxxxxx171//尾插法创建链表2bool insertTail(linkList &l){3lNode *pHead,*pTial; //指针pHead和pTial分别表示链表头部和尾部4pTial=l; //将尾指针指向l链表5int i=0;6while(i!=999999){7cin>>i;8if(i!=999999){9pHead=(lNode*)malloc(sizeof(lNode));10pHead->data=i; //创建结点pHead其数据与为输入的i值11pTial->next=pHead; //将尾部结点的指针域指向头部结点12pTial=pHead; //接着将尾部结点指向创建的头部结点13}14}15pTial->next=NULL; //将最后一个指针域设置为空16return 1;17}主函数:
xxxxxxxxxx51int main(){2linkList link;3initList(link); //链表初始化4insertTail(link); //尾插法创建链表5}
运行结果:
输入:1,2,399

4.1.2 头插法建立链表
头插法将每个数据插入在链表头部。头插法可以用于链表的逆置。
同样先初始化链表:
xxxxxxxxxx131typedef struct LNode{2int data; //定义单链表结点类型3struct LNode *next; //每个节点存放一个数据元素4}lNode,*linkList; //指针指向下一个节点56//初始化链表7bool initList(linkList &l){8l=(lNode*)malloc(sizeof(lNode)); //链表开辟一个头节点9if(l==NULL)10return false;11l->next=NULL; //头结点指针域指向空12return true;13}创建链表:
xxxxxxxxxx141bool insertHead(linkList &l){2int i=0;3lNode *p;4while(i!=999999){5cin>>i;6if(i!=999999){7p=(lNode*)malloc(sizeof(lNode));8p->data=i;9p->next=l->next;10l->next=p;11}12}13return 1;14}主函数
xxxxxxxxxx51int main(){2linkList link;3initList(link); //链表初始化4insertHead(link); //尾插法创建链表5}
运行效果和尾插法一样。
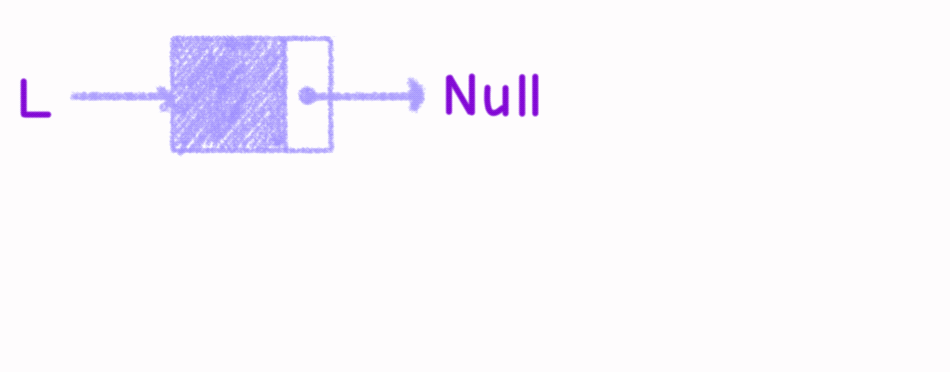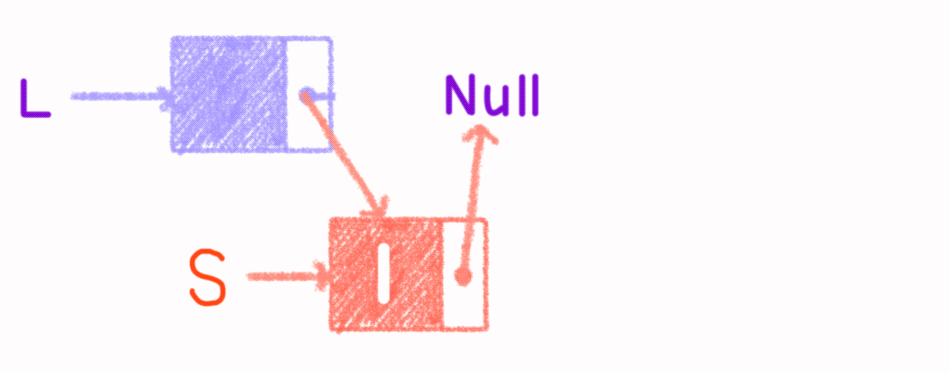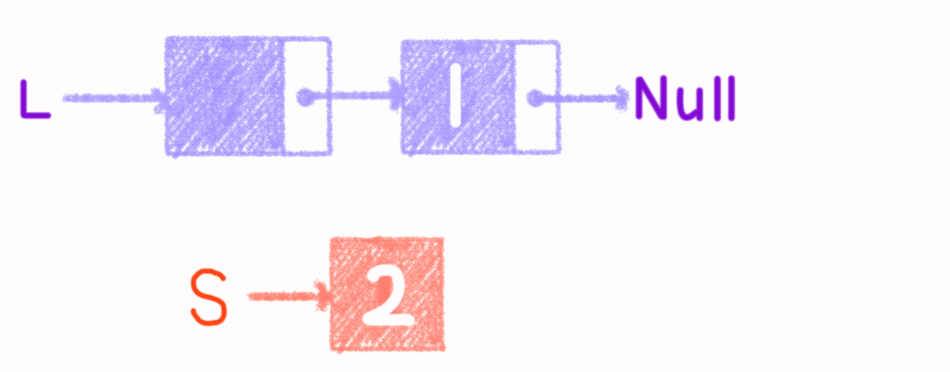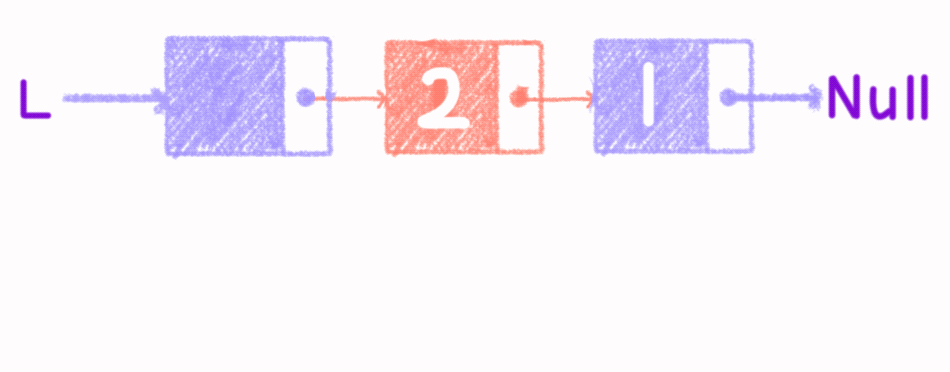
4.2 单链表的插入
核心思路是将插入位置前一个结点的指针域指向新建立的结点,再将新节点的指针与指向后一个结点(前一个结点指针域中的值为后一个结点)。
代码如下:
xxxxxxxxxx251//按序号插入2bool insertVaule(linkList &l,int local,int e){ //local表示要插入位置,e表示插入的值3 lNode *p,*head=l; 4 int i;5 p=(lNode*)malloc(sizeof(lNode));6 if(p==NULL||local<1) return 0;7 p->data=e; //建立新节点p8 while(head->next!=NULL&&i<local-1){ //找到要插入位置的上一个结点9 head=head->next;10 i++;11 }12 p->next=head->next; //将新节点p的指针域指向后一个结点13 head->next=p; //前一个结点指针域指向新节点p14 return 1;15} 16//前插操作:将s结点插入到p结点之前17bool InsertPriorNode (LNode *p,LNode *s){18 if (p==NULL||S==NULL) return false;19 s->next=p->next; //s指针与连接到p结点的后继20 p->next=s; //s连到p之后21 ElemType temp=p->data; //交换数据域部分22 p->data=s->data;23 S->data=temp;24 return true;25}主函数:
xxxxxxxxxx71int main(){2 linkList link;3 initList(link); //链表初始化 4 insertTail(link); //尾插法创建链表 5 insertVaule(link,3,66); //按号插入 6 printlist(link); //链表遍历 7} 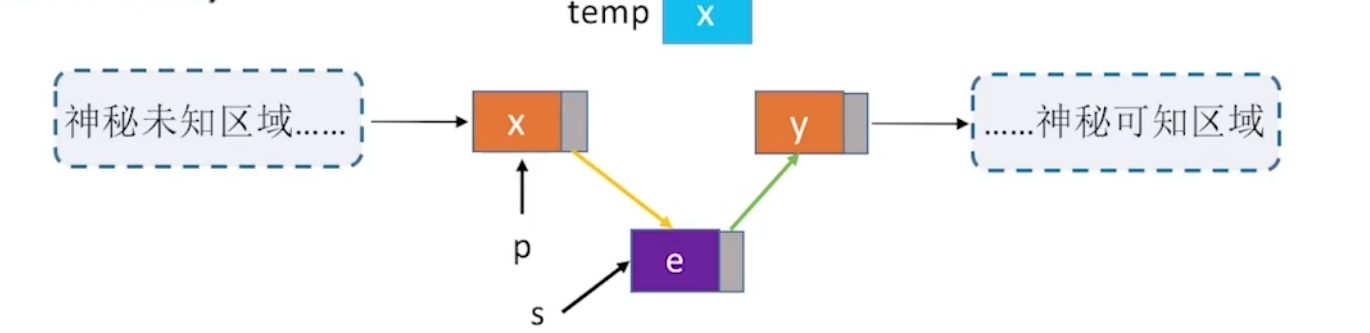
输入:1,2,3,4,5
运行结果:1,2,3,66,4,5
4.3 单链表的删除
通过按照输入序号删除对应结点,其原理和上面的插入类似。
xxxxxxxxxx251//按序号删除2bool deletaList(linkList &l,int number){3 int i=0;4 lNode *p=l,*tail; //tail指针存放的要删除的结点5 if(number<=0){6 return 0;7 }8 while(p!=NULL&&i<number-1){ //找到删除结点的前一个结点9 p=p->next;10 i++;11 }12 tail=p->next; //将tail指向要删除结点地址13 p->next=tail->next; //将前一个结点指针域指向被删除结点后一个结点14 free(tail); //释放要删除结点15 return 1;16} 17//删除指定结点p18bool DeleteNode (LNode *p){19 if (p==NULL) return false;20 LNode *q=p->next; //令q指向*p的后继结点21 p->data=p->next->data; //和后继结点交换数据域22 p->next=q->next; //将*q结点从链中“断开”23 free(q); //释放后继结点的存储空间24 return true;25}主函数代码:
xxxxxxxxxx71int main(){2 linkList link;3 initList(link); //链表初始化 4 insertTail(link); //尾插法创建链表 5 deletaList(link,3); //按序号删除6 printlist(link); //链表遍历 7} 关于删除指定节点p,其本质就是将p的后继结点复制给p结点,再释放后继结点,并将p结点重新指向下一个结点。这种方法有个局限性,就是我们在删除最后一个结点时,由于后一个结点为null所以程序会出错,我们就只能使用传统办法循环一个个找了。
输入:1,2,3,4,5
运行结果:1,2,4,5
4.4 链表的查找
最常用的查找是按值查找和按序号查找
xxxxxxxxxx331//按值查找2bool findVaule(linkList &l,int d){ //d代表要查找的值3 lNode *p=l;4 while(p!=NULL){5 if(p->data==d){ //如果找到要查找的值d返回16 return 1;7 }8 p=p->next;9 }10 return 0;11 12} 13
14//按号查找15int findNumber(linkList &l,int num){//表示返回第num个结点的值16 int i=0;17 if(num<=0){18 return 0;19 }20 lNode *p=l;21 while(p!=NULL&&i<num){ //找到这个结点,并返回结点值域中的值22 p=p->next;23 i++;24 }25 return p->data;26} 27//对单链表进行打印 28void printlist(linkList &l){29 while(l->next!=NULL){30 cout<<l->next->data<<endl;31 l=l->next;32 }33}主函数:
xxxxxxxxxx111int main(){2 linkList link;3 initList(link); //链表初始化 4 insertTail(link); //尾插法创建链表 5 int resultVaule,resultNumber;6 resultVaule=findVaule(link,2); //按值查找 7 cout<<resultVaule<<endl;8 resultNumber=findNumber(link,3);//按序号查找 9 cout<<resultNumber<<endl;10 printlist(link); //链表遍历 11} 4.5 习题:链表的逆置
逆置方法有很多种:
方法一:可以通过遍历链表元素,用头插法将遍历元素值插入新链表。
xxxxxxxxxx621using namespace std;4typedef struct lNode{5 int data;6 lNode *next;7}lNode,*linkList;8
9//初始化10bool initLink(linkList &l){11 l=(lNode*)malloc(sizeof(lNode));12 if(l==NULL) return 0;13 l->next=NULL;14 return true;15} 16
17//尾插法18bool insertTail(linkList &l){19 int i=0;20 lNode *head,*tial=l;21 while(i!=999999){22 cin>>i;23 if(i!=999999){24 head=(lNode*)malloc(sizeof(lNode));25 head->data=i;26 tial->next=head;27 tial=head;28 }29 }30 tial->next=NULL;31 return 1;32}33 34 //头插法实现逆序35lNode* reverseLink(linkList &l){36 lNode *p,*r;37 initLink(r);38 while(l->next!=NULL){ //遍历链表取值39 p=(lNode*)malloc(sizeof(lNode));40 p->data=l->next->data; //头插法赋值给新链表41 p->next=r->next;42 r->next=p;43 l=l->next; 44 }45 return r;46} 47 48 //打印链表49 void printLink(linkList &l){50 while(l->next!=NULL){51 cout<<l->next->data<<endl;52 l=l->next;53 }54 } 55 56int main(){57 lNode *link,*result;58 initLink(link); //初始化链表 59 insertTail(link); //尾插法创建列表60 result=reverseLink(link); //用头插法实现逆序61 printLink(result);62}输入值:1,23,4,5
运行结果:5,4,23,1
方法二:
方法是先让新结点p=l->next,
再让头节点指针l->next=NULL断开链表。
用结点lNodeNext=p来记录结点p,p=p->next指向下一轮待逆置的结点。
最后让lNodeNext用头插法插在l链表内即可
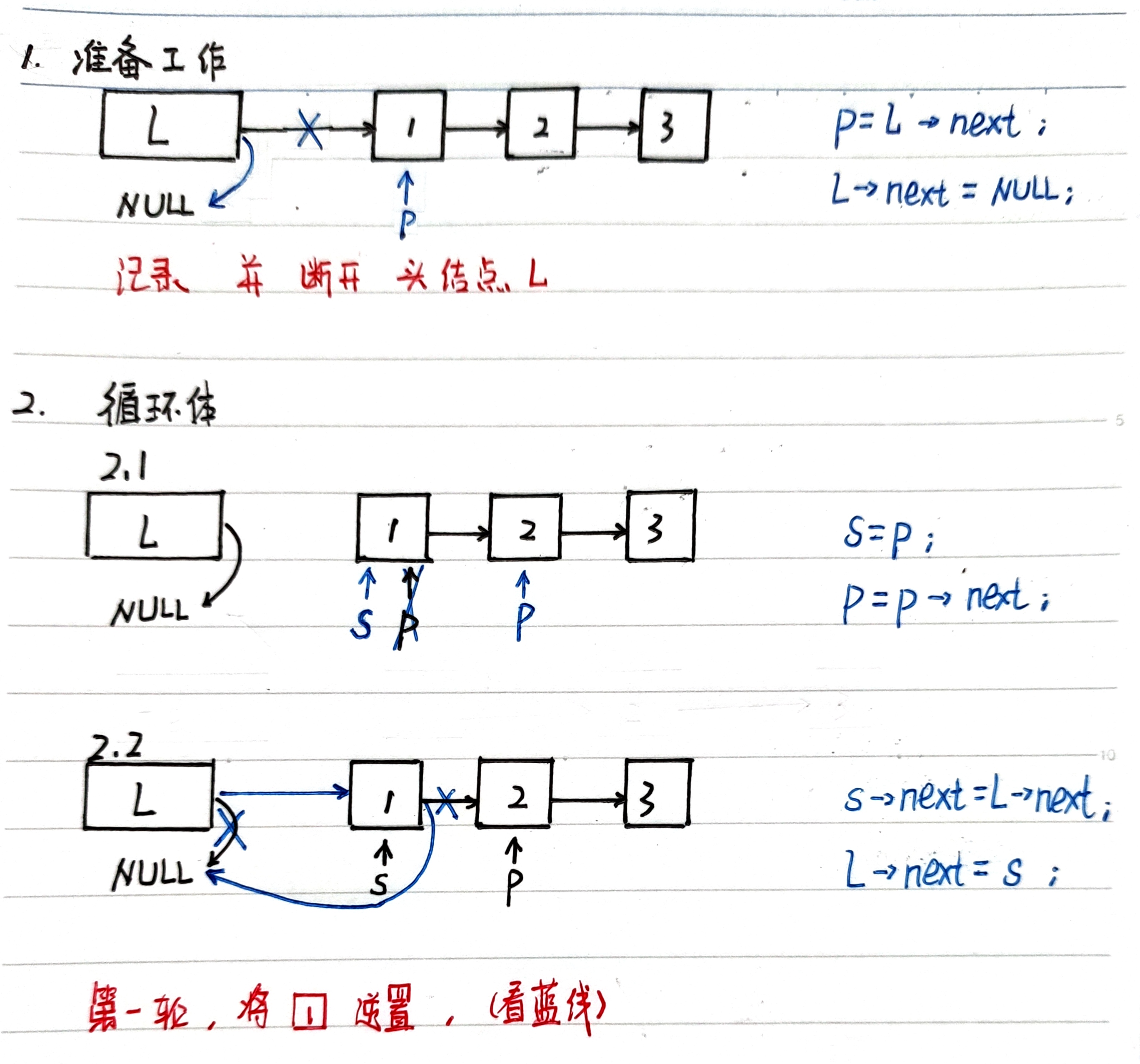
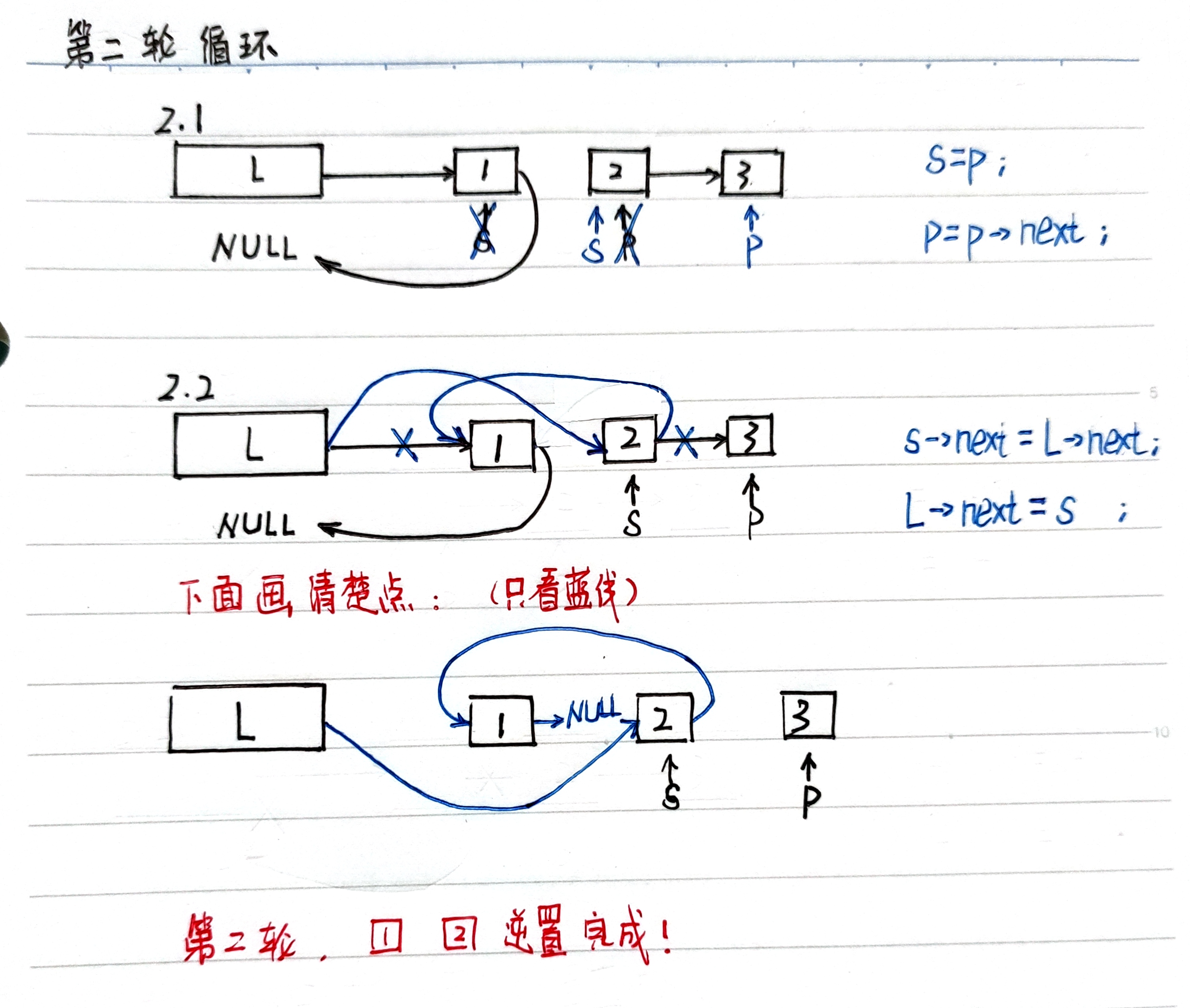
xxxxxxxxxx231//链表的逆置2void changeList(linkList &l){ 3 lNode *lTem=l,*p=l->next,*qNextLNode;4 lTem->next=NULL;5 while(p!=NULL){6 qNextLNode=p;7 p=p->next; 8 qNextLNode->next=lTem->next;9 lTem->next=qNextLNode;10 }11
12} 13
14int main(){15 linkList link6;16 initList(link6);17 //链表的逆置18 cout<<"请输入一组链表进行逆置:"<<endl;19 createList(link6);20 cout<<"逆置后的链表为:"<<endl;21 changeList(link6);22 myPrint(link6);23}输入值:1,23,4,5
运行结果:5,4,23,1
5. 双链表
由于单链表只能指向下一个指针,而双链表同时指向前驱节点和后继结点。
5.1 双链表的初始化
xxxxxxxxxx181typedef struct DNode{ //定义双链表结点类型2 ElemType data; //数据域3 struct DNode *prior,*next; //前驱和后继指针4}DNode, *DLinklist;5
6//初始化双链表7bool InitDLinkList(DLinklist &L){8 L = (DNode *) malloc(sizeof (DNode)); //分配一个头结点9 if (L==NULL) return false; //内存不足, 分配失败10 L->prior = NULL; //头结点的prior永远指向NULL11 L->next = NULL; //头结点之后暂时还没有节点12 return true;13}14void testDL inkList() { //初始化双链表15 DLinklist L;16 InitDLinkList(L);17 //后续代码...18}同样的这里的DNode和DLinklist等价,只是为了区分链表(DLinklist)和结点(DNode)
5.2 双链表的插入
xxxxxxxxxx101//在p结点之后插入s结点.2bool InsertNextDNode(DNode *p,DNode *s){3 if (p==NULL||s==NULL) return false; //非法参数4 s->next=p->next;5 if (p->next != NULL) 6 p->next->prior=s; //如果p结点有后继结点7 s->prior=p;8 p->next=s;9 return true;10}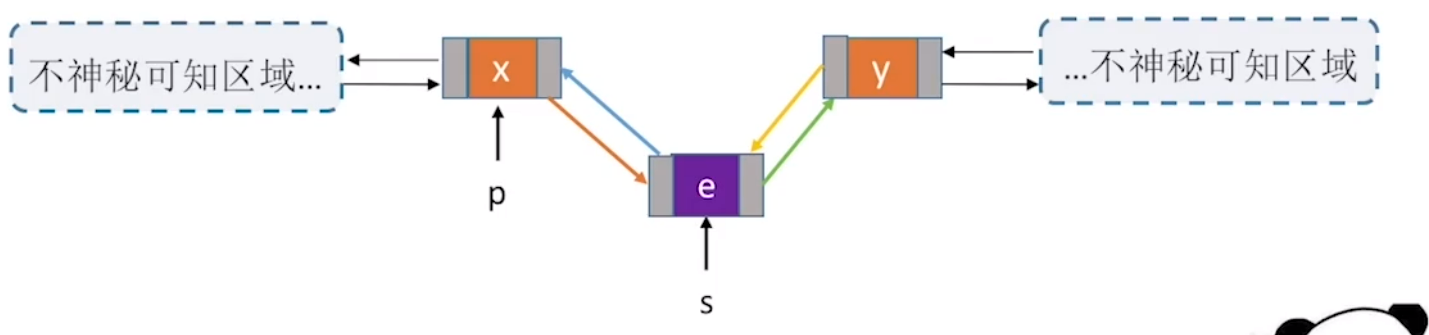
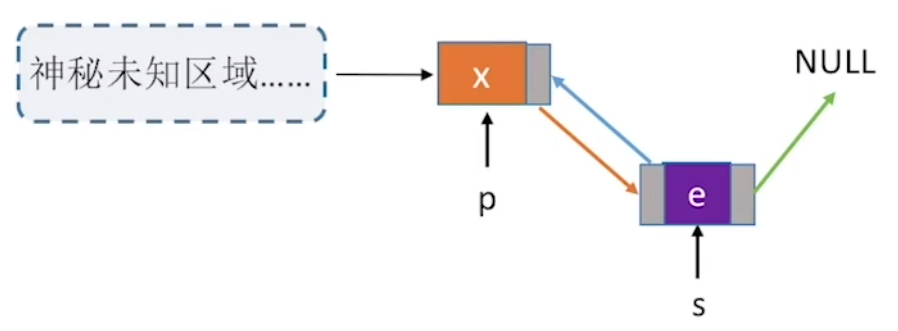
5.3 双链表的删除
同样和之前但链表删除方法一致。
xxxxxxxxxx191//删除p结点的后继结点q2bool DeleteNextDNode(DNode *p){3 if ( p==NULL) return false;4 DNode *q = p->next; //找到p的后继结点q5 if (q==NULL) return false; //p没有后继6 p->next=q->next;7 if (q->next !=NULL) //q结点不是最后一个结点8 q->next->prior=p;9 free(q); //释放结点空间10 return true; 11}12
13//双链表的销毁14void DestoryL ist(DLinklist &L){ //循环释放各个数据结点15 while (L->next != NULL)16 DeleteNextDNode(L); //删除每个结点的后一个结点17 free(L); //释放头结点18 L=NULL; //头指针指向NULL 19}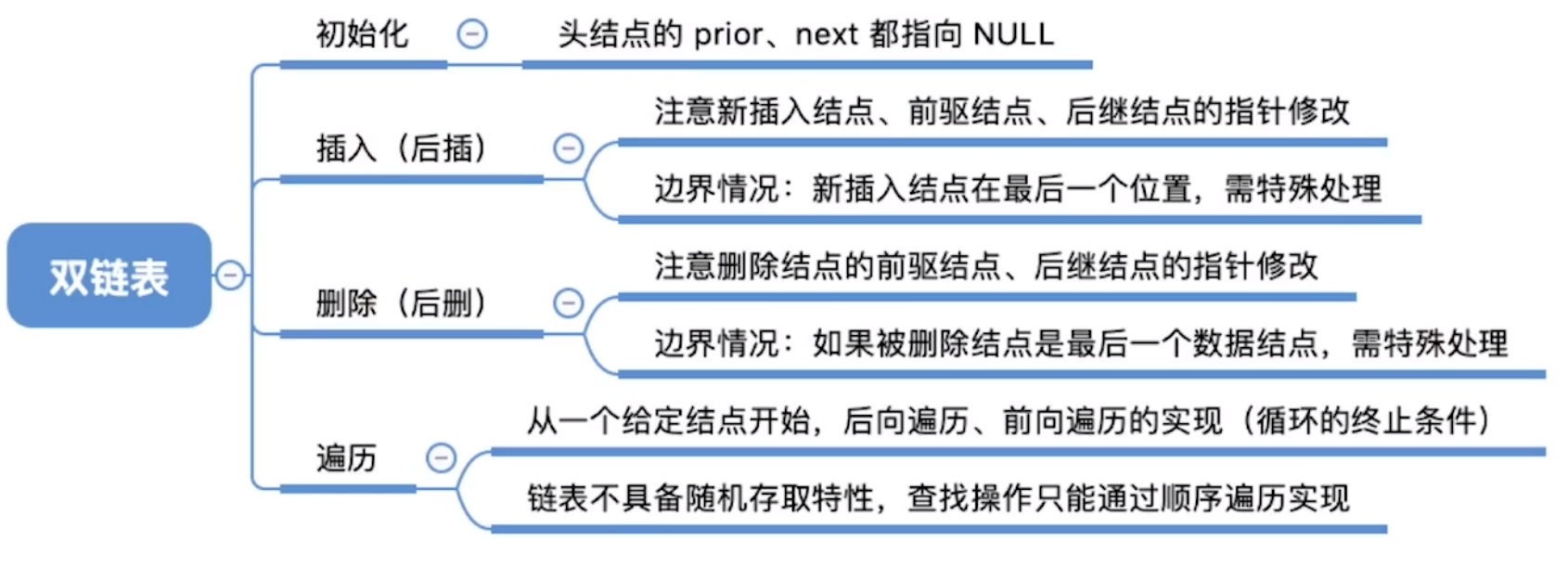
6. 循环链表
循环链表就是在单链表(双链表)的基础上讲最后一个结点指向头节点。
特点是:从一个结点出发可以找到其他任何一个结点。常用于对表头和表尾操作频率高的情况下。
6.1 循环单链表的初始化

xxxxxxxxxx111typedef struct LNode{ //定义单链表结点类型2 ElemType data; //每个节点存放一个数据元素3 struct LNode *next; //指针指向下一个节点4}LNode, *LinkList;5//初始化一个循环单链表6bool InitList(LinkList &L) {7 L = (LNode *) malloc(sizeof(LNode)); //分配一个头结点8 if (L==NULL) return false; //内存不足,分配失败9 L->next = L; //头结点next指向头结点本身10 return true; 11}其他操作基本与前面一致。注意判断最后一个结点时,应该判断是否指向头节点。
6.2 循环双链表的初始化
循环链表:表头结点的prior指向表尾结点;表尾结点的next指向头结点。
循环双链表不需要考虑表头表尾的界限操作。

xxxxxxxxxx131typedef struct DNode{ //定义双链表结点类型2 ElemType data; //数据域3 struct DNode *prior,*next; //前驱和后继指针4}DNode, *DLinklist;5
6//初始化空的循环双链表7bool InitDL inkList(DLinklist &L){8 L = (DNode *) malloc(sizeof(DNode)); //分配一个头结点9 if (L==NULL) return false; //内存不足,分配失败10 L->prior = L; //头结点的prior指向头结点11 L->next = L; //头结点的next指向头结点12 return true;13}其他操作
xxxxxxxxxx121//在p结点之后插入s结点2bool InsertNextDNode(DNode *p,DNode *s){3 s->next=p->next; //将结点*s插入到结点*p之后4 p->next->prior=s;5 S->prior=p;6 p->next=s;7}8
9//删除p的后继结点q10p->next=q->next;11q->next>prior=p;12free(q);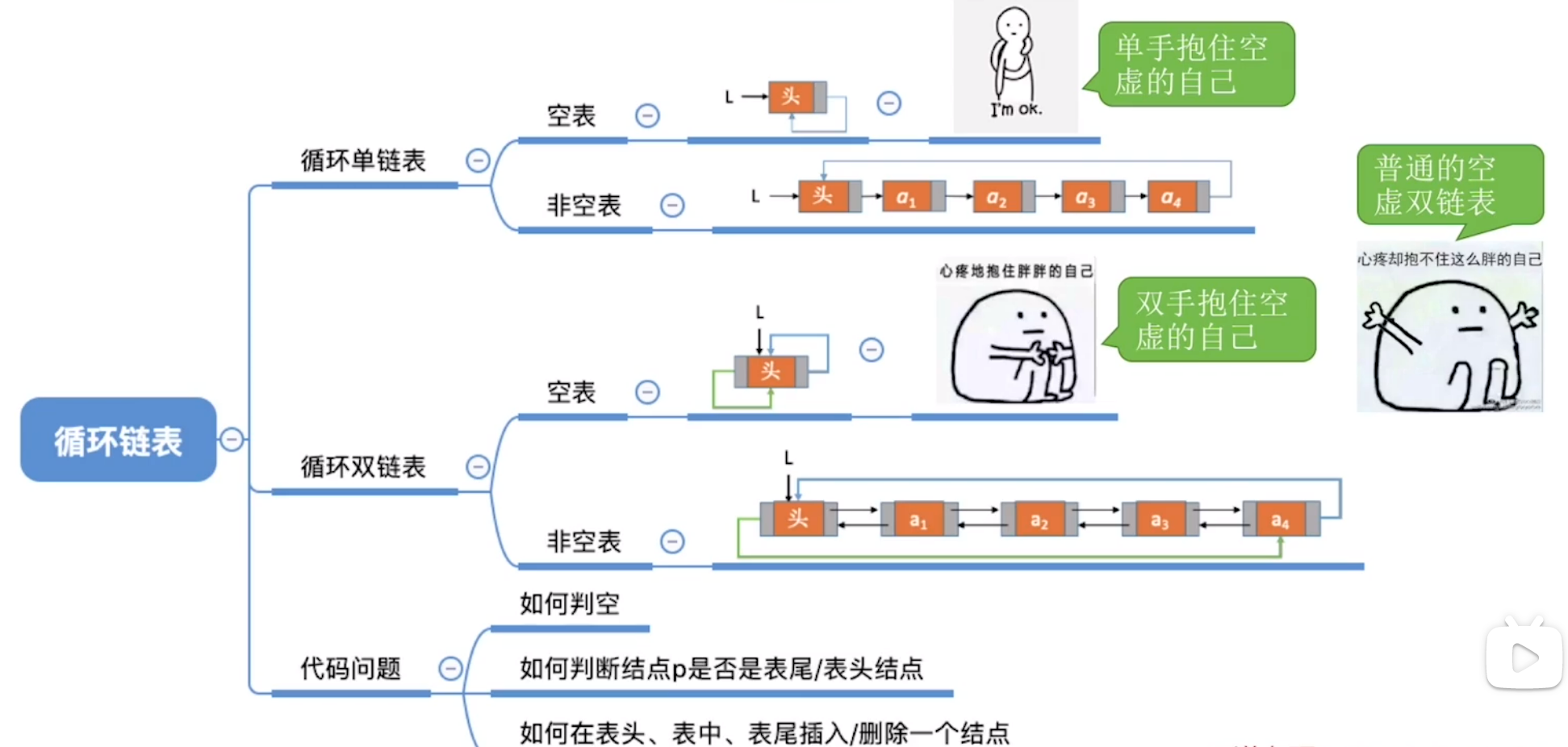
7. 静态链表
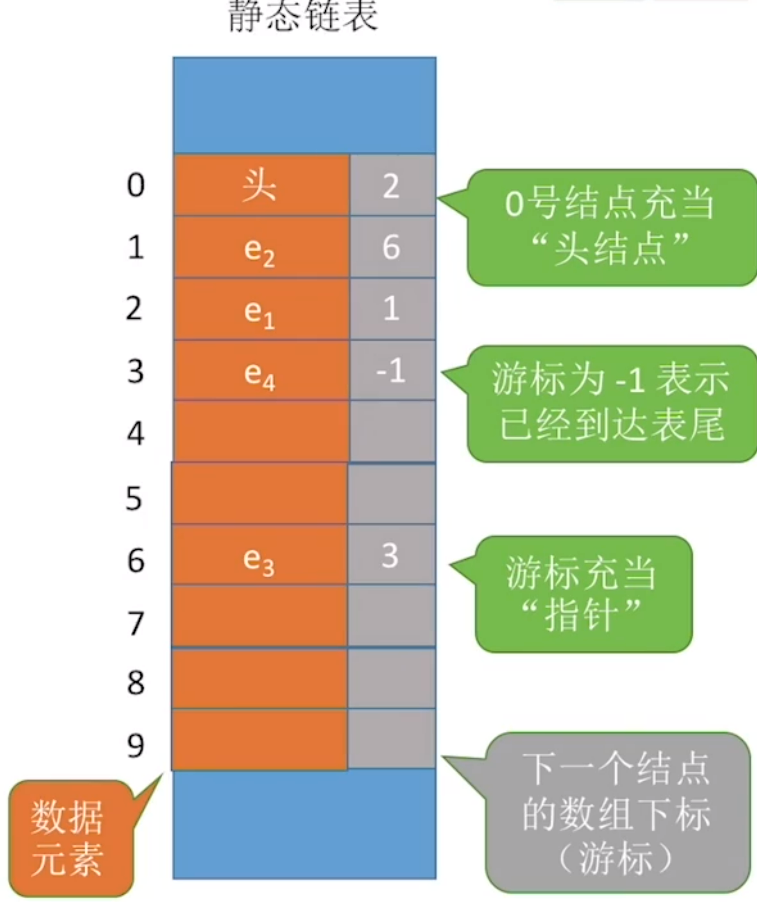
与单链表不同的是静态链表是分配一整片连续的内存空间,各个结点集中安置。
静态链表每个数据元素4B,每个游标4B ( 每个结点共8B)。设起始地址为addr,e1的存放地址为addr + 8*2。2是接下来要寻找的数组下标。
适用场景:①不支持指针的低级语言;②数据元素数量固定不变的场景(如操作系统的文件分配表FAT)。
7.1 静态链表的初始化
xxxxxxxxxx161 4typedef char elemtype;5typedef struct{6 int cur;7 elemtype data;8}slink,slinklist[maxsize];9
10void initspace_sl(slink *space){//将数据各分量链接成一个备用链表,space[0]代表头指针11 int i;12 for(i=0;i<maxsize-1;i++){13 space[i].cur=i+1; //下标为i结点的后继为下标是i+1的结点14 }15 space[maxsize-1].cur=0; //0表示空指针16} 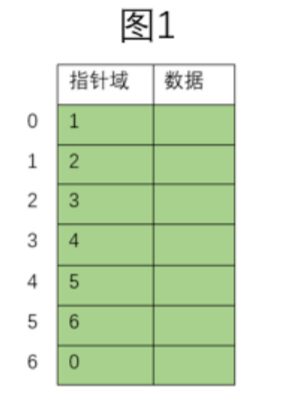
8. 顺序表和链表的比较
两种表的适用场景:
- 表长难以预估、经常要增加
- 表长可预估、查询(搜索)操作较多用顺序表(课堂点名)。
逻辑结构:顺序表和链表都属于线性结构。
存储结构:
- 顺序表优点:拥有随机存取的特点,存储密度高。缺点:大片连续空间分配不方便,改变容量不方便。
- 链表优点:离散的小空间分配方便,改变容量方便。缺点:不可随机存储,存储密度低。
基本操作比较:
两种表的创建:
顺序表:需要预分配大片连续空间。若分配空间过小,则之后不方便拓展容量;若分配空间过大,则浪费内存资源。
静态分配:容量不可更改。
动态分配:容量可以更改,但需要移动大量元素,时间代价高。
链表:只需分配一个头结点(也可以不要头结点,只声明一个头指针),之后方便拓展
两种表的销毁:
链表:依次删除各个结点(free)
顺序表:需要讲
注意:malloc和free函数必须成对出现。
两种表的增加和删除
- 顺序表:插入
- 链表:插入
- 顺序表:插入
两种表的查找
- 顺序表:按位查找时间复杂度为
- 链表:按位查找和按值查找时间复杂度都为
- 顺序表:按位查找时间复杂度为
在遇到一个开放式问题探讨时:从逻辑结构,存储结构和基本操作这三方面回答。
四. 栈
栈和线性表的结构很相似,但栈只允许在一端进行插入或删除操作的线性表。栈和我们生活种摞起来的盘子类似。

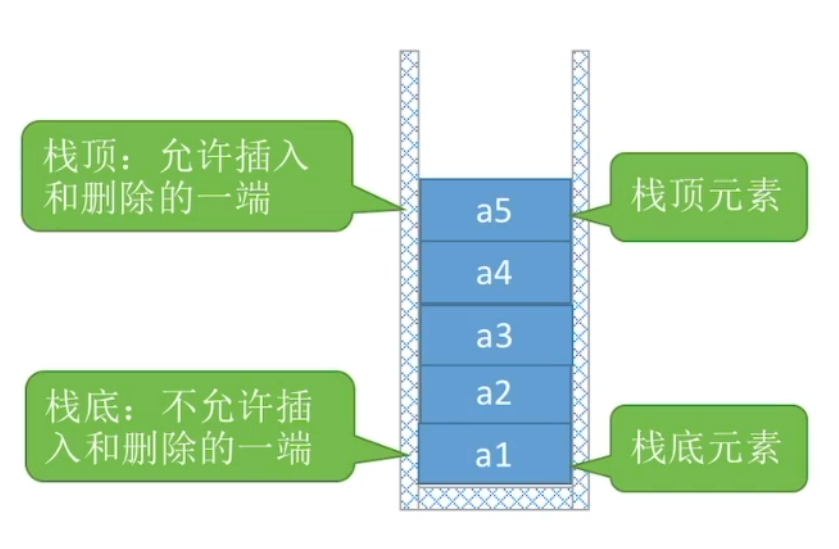
进栈顺序:
出战顺序:
栈特点:后进(push)先出(pop)(LIFO)
栈的基本操作:创建、销毁、增加、删除、查询、判空。
1. 栈的顺序存储实现
1.1 栈的定义
和线性表类似,我们先要用结构体初始化栈。
xxxxxxxxxx181//定义栈中元素的最大个数2typedef struct{3 ElemType data [MaxSize];//静态数组存放栈中元素4 int top; //栈顶指针,每次入栈值+1,永远指向栈顶5} SqStack;6
7//初始化栈8void InitStack(SqStack &S){9 S.top=-1; //初始化栈顶指针 10}11
12//判断栈空13bool StackEmpty(SqStack S){14 if(S. top==-1)15 return true; //栈空16 else 17 return false; //不空18}1.2 栈的增加
xxxxxxxxxx91//新元素入栈2bool Push(SqStack &s, ElemType x){3 if(s.top==MaxSize-1)4 return false; //栈满,报错5 s.top = s.top+1; //指针先加1 6 s.data[s.top]=x; //新元素入栈 7 //上面两句等价于:s.data[++s.top]=x;8 return true;9}1.3 出栈操作
xxxxxxxxxx91//出栈操作2bool Pop(SqStack &S, ELemType &x){3 if(S.top==-1) //栈空,报错 4 return false;5 x=S.data[S.top]; //栈顶元素先出栈 6 S.top=S.top-1; //指针再减l7 //等价于:x=S.data[s.top--];8 return true;9}1.4 共享栈
通过上面代码实现我们可以发现栈的一个明显缺点是栈的大小不可变,可以通过链式栈或者分配大空间来解决这个问题。但分配大片空间会导致空间冗余,这时候可以用共享栈解决。
共享栈就是两个栈共享一片空间。
共享栈实现:
xxxxxxxxxx131//定义栈中元素的最大个数3typedef struct{4 ElemType_ data [MaxSize]; //静态数组存放栈中元素5 int top0; //0号栈栈顶指针 6 int top1; //1号栈栈顶指针7} ShStack;8
9//初始化栈10void InitStack(ShStack &S){11 S.top0=-1; //初始化栈顶指针 12 S.top1=MaxSize;13}
共享栈两个top指针一个从下网上存储,一个从上往下存储。判断栈满的条件是:top0 + 1 == top1
2. 链栈
定义:用链式存储结构实现的栈
实现:实际上我们用头插法建立的单链表就是一个链栈。
2.1 链栈初始化
xxxxxxxxxx121typedef struct Linknode{2 ElemType data; //数据域3 struct L inknode *next; //指针域4} *LiStack; //栈类型定义5
6//初始化 7bool initStack(LiStack &l){8 l=(LiStack)malloc(sizeof(LiStack));//带头节点9 if(l==NULL) return false;10 l->next=NULL;11 return true;12}2.2 链栈的入栈
用头插法入栈
xxxxxxxxxx91bool pushStack(LiStack &l,int e){2 if(l==NULL) return false;3 LiStack p;4 p=(LiStack)malloc(sizeof(LiStack));5 p->data=i; //头插法6 p->next=l->next;7 l->next=p;8 return true;9} 2.3 链栈的出栈
链栈的出栈操作,栈顶指针是第一个指针(头指针的下一个),所以将其往后挪一位就好了。
xxxxxxxxxx121//出栈2bool Pop(LiStack &l){3 LiStack p;4 if(l->next==NULL){5 return false;6 }else{7 p=l->next; //p指向第一个结点(头结点后继结点)8 l->next=p->next; //往后挪一位9 free(p);10 return true;11 }12}2.4 链栈打印
最后其它操作和单链表一致。
xxxxxxxxxx61void printStack(LiStack &l){2 while(l->next!=NULL){3 cout<<l->next->data<<endl;4 l=l->next;5 }6} 3. 栈的应用—括号匹配
括号匹配就是相邻括号成对出现。如:
具体思路是用栈实现括号匹配:
- 依次扫描所有字符,遇到左括号入栈,遇到右括号存入数组(也可以不用数组,当输入右括号直接和栈中括号匹配)
- 查看是否匹配。匹配失败情况: ①左括号单身②右括号单身③左右括号不匹配
xxxxxxxxxx851using namespace std;5
6static int couts=0; //全局静态变量,用于记录数组中的右括号数 7typedef struct Linknode{8 char data; 9 struct Linknode *next; 10} *LiStack; 11
12//初始化13bool initLiStack(LiStack &l){14 l=(LiStack)malloc(sizeof(LiStack));15 if(l==NULL) return false;16 l->next=NULL;17 return true;18} 19
20//入栈21bool pushStack(LiStack &l,char s){22 LiStack p;23 p=(LiStack)malloc(sizeof(LiStack));24 if(p==NULL) return false;25 p->data=s;26 p->next=l->next;27 l->next=p;28 return true;29}30
31//出栈 32char popStack(LiStack &l){ 33 LiStack p;34 char s;35 if(l->next==NULL) {36 cout<<"栈空"<<endl;37 return 'E'; 38 }39 s=l->next->data;40 p=l->next;41 l->next=p->next;42 free(p);43 return s; 44}45
46//区分左右括号47void bracketLeftRight(LiStack &l,char *p,char str){ //p表述指针数组,str用户输入值 48 if(str=='('||str=='{'||str=='['){ //如果是左括号,放入栈中 49 pushStack(l,str);50 }else if(str==')'||str=='}'||str==']'){ //如果是右括号,放入数组中,全局变量couts+1 51 p[couts]=str;52 couts+=1;53 }else{54 cout<<"输入值不合法"<<endl;55 } 56 }57 58 //判断括号是否对应59 bool bracketCheck(LiStack &l,char *p){60 char bracket;61 for(int j=0;j<couts;j++){62 bracket=popStack(l);63 if(bracket=='E') return false; //栈空,配对失败 64 if(p[j]==')'&&bracket!='(') return false; //三种括号匹配 65 if(p[j]==']'&&bracket!='[') return false;66 if(p[j]=='}'&&bracket!='{') return false;67 }68 }69
70int main(){71 LiStack l; 72 char str,c[MaxSize]={0},*p=c; //str:接受输入值,c[]存放右括号,p数组指针传递 73 initLiStack(l); //初始化 74 while(str!='!'){ //输入'!'结束输入 75 cin>>str;76 if(str!='!'){77 bracketLeftRight(l,p,str); //每输入一个值判断左右括号 78 }79 }80 if(bracketCheck(l,p)>0){81 cout<<"括号全部匹配"<<endl; //括号全部匹配 82 }else{83 cout<<"括号不匹配"<<endl; //括号不匹配 84 } 85} 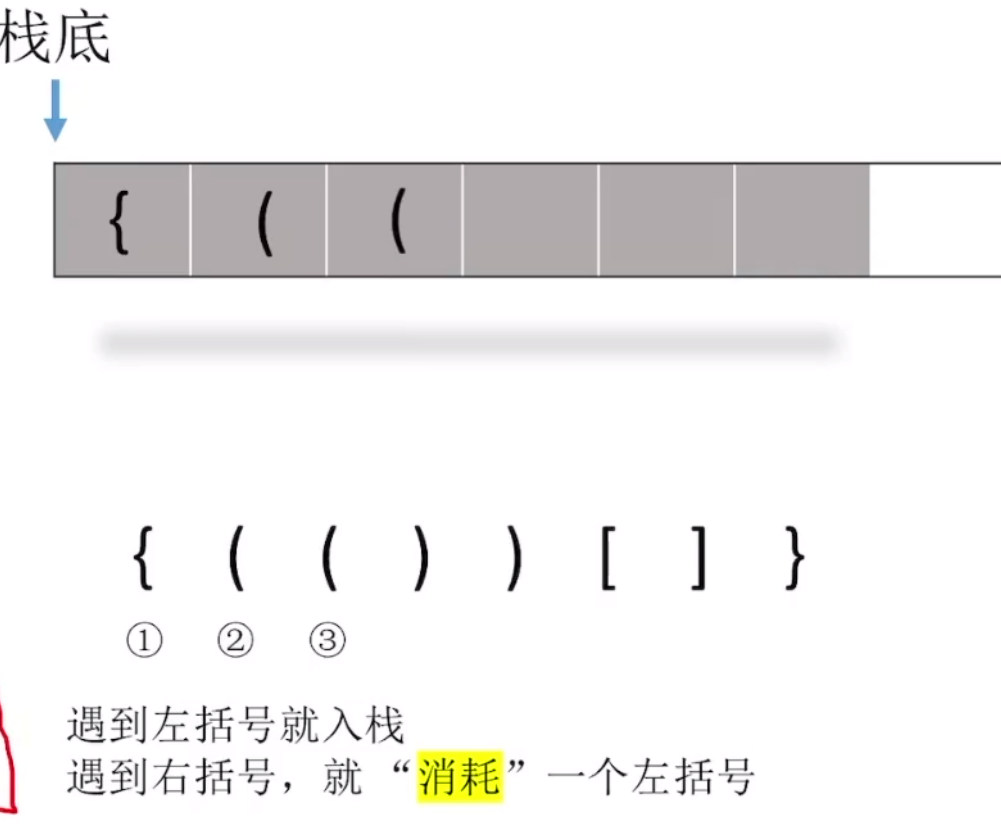
4. 栈的应用—表达式求值
表达式通常由三部分组成:①操作数②运算符③界限符(括号等)
常见表达式有以下几种:
中缀表达式:
特点:运算符在两个数中间
后缀表达式(逆波兰表达式):
特点:运算符在两个操作数后面
前缀表达式(波兰表达式):
特点:运算符在操作数前面
4.1 中缀表达式转后缀方法
遵循左优先原则。
①确定运算顺序
②选择下一个运算符,按照
③如果还有运算符没被处理,继续②
如
4.2 后缀表达式计算
通过上面我们将中缀表达式转为后缀表达式
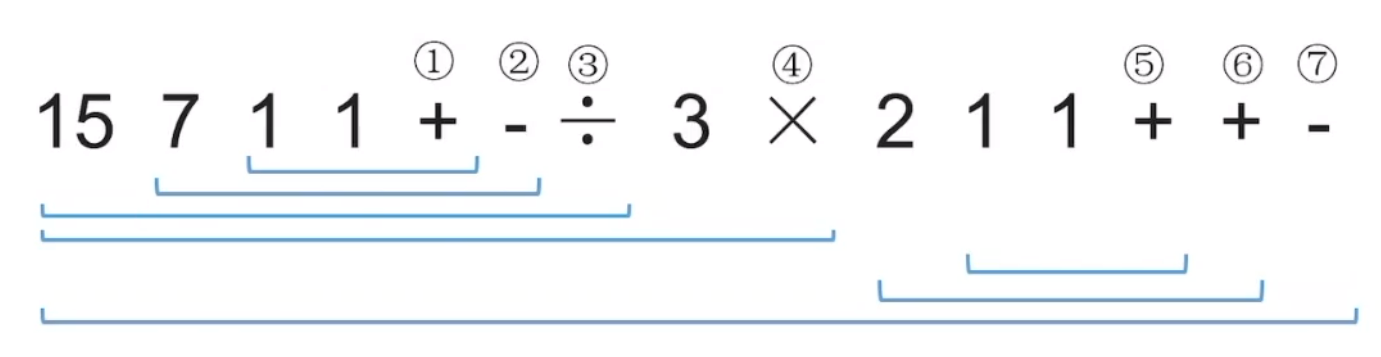
计算后缀表达式也不难:从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算 合体为一个操作数。注意:两个操作数的左右顺序。
步骤:
- 第一个运算符是
- 第二个运算符是
- 第三个运算符是
- 第四个运算符是
- 第五个运算符是
- 第六个运算符是
- 最后一个运算符是
4.3 代码实现
代码实现需要遵循以下几点:
①遇到操作数直接入栈
②遇到界限符'
③运算符运算弹出规则,应该是:操作符栈顶运算符大于或等于当前输入运算符则弹出栈顶操作符。数字栈依次弹出两个数字
Ⅰ.先分析运算符生效顺序,如下图:

Ⅱ. 从左到右依次扫描入栈:操作符栈(charStack),操作数栈(numStack)
Ⅲ. 定义操作符优先级:
Ⅳ. 进行扫描运算:
①输入'
',由于操作符栈为 ,直接入栈。 ②输入'
',操作符栈不为 ,且优先级等于操作栈顶的元素'(',但由于括号不参与运算,所以直接入栈。 ③输入
,数字直接入栈。 ④输入'
',由于'÷'优先级低于操作符栈顶元素'(',直接入栈。 ⑤输入'
',括号直接入栈。 ⑥输入
,数字直接入栈。 ⑦输入'
',' '优先级低于操作符栈顶元素' ',入栈。 ⑧输入'
',直接入栈 ⑨输入
,入栈 ⑩输入'
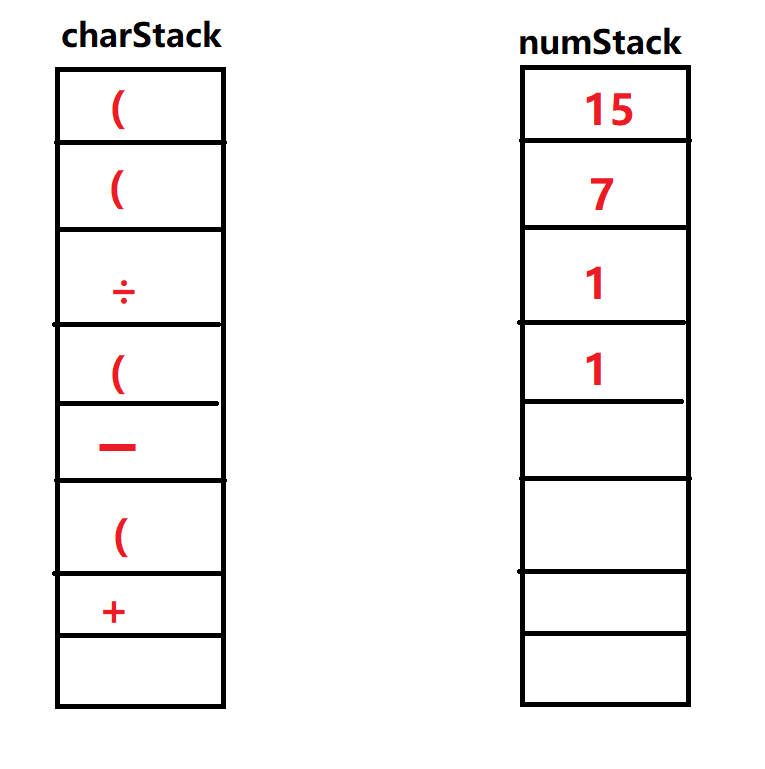
',' '优先级低于操作符栈顶元素' ',入栈 ⑪输入
,入栈。此时栈中元素情况如下:
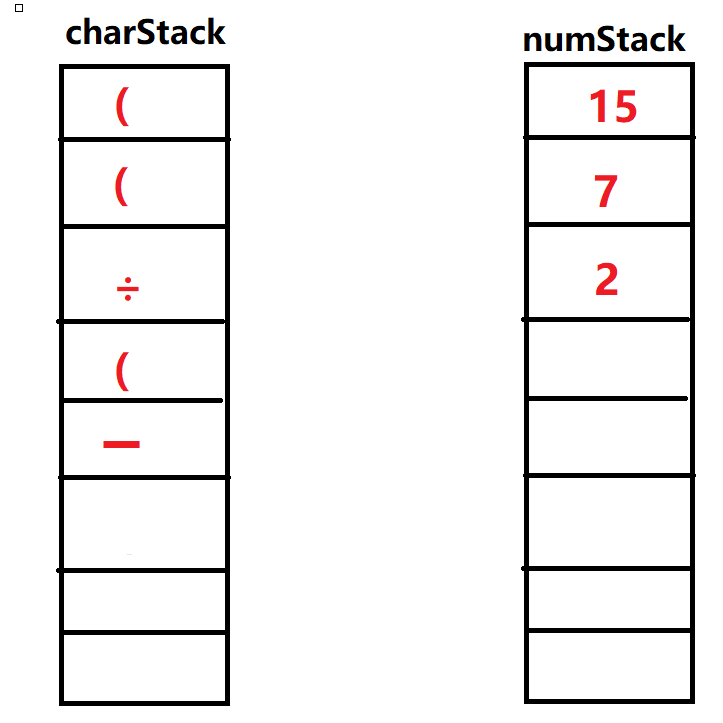
⑫输入'
',栈顶操作符一次出栈直到为NULL或者为' '。此时弹出操作符栈顶元素' ',弹出操作数栈前两个元素 。之后运算 得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
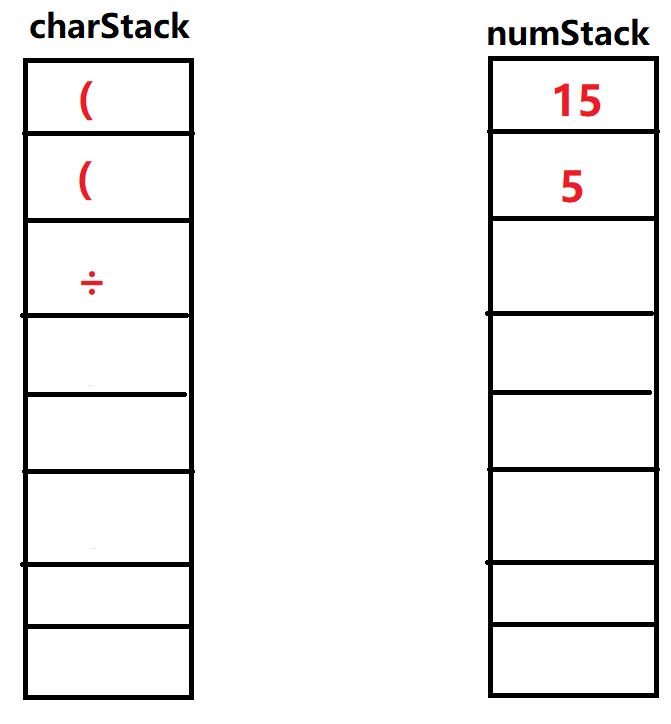
⑬输入')',再次重复上面,弹出操作符栈顶元素'
',弹出操作数栈两个元素 ,运算 。得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
⑭输入'
',重复上面过程,弹出操作符栈顶元素' ',弹出操作数栈两个元素 ,运算 。得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
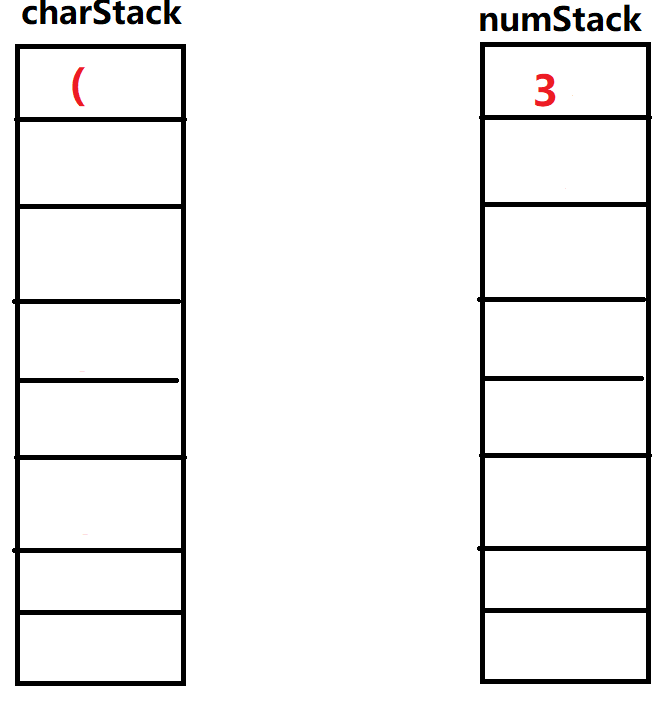
⑮输入'
',此时操作符栈顶元素为' ',优先级低于栈顶元素,直接入栈。 ⑯输入'
',直接入栈
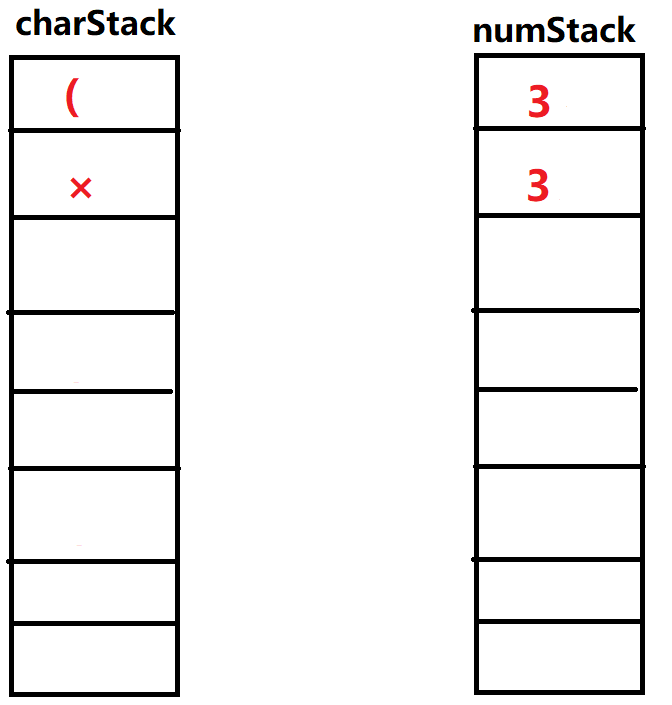
⑰输入'
',弹出操作符栈顶元素' ',弹出操作数栈两个元素 ,运算 。得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
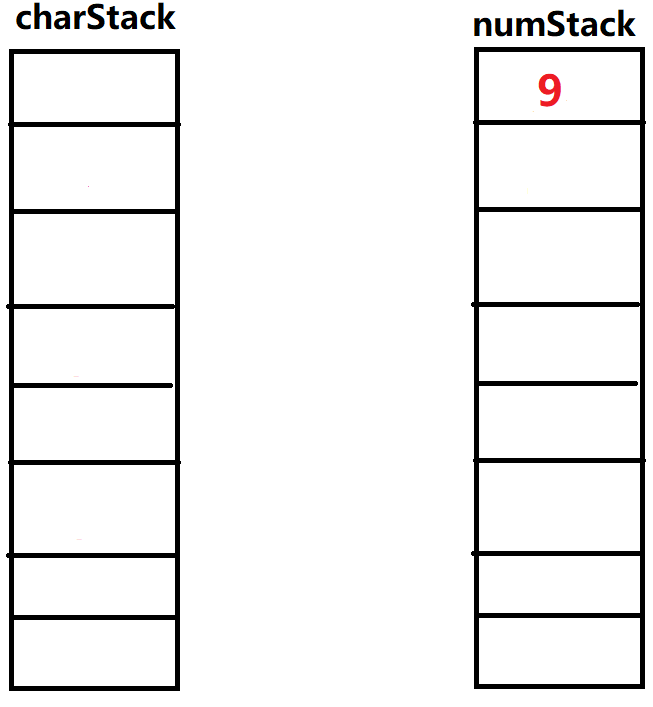
⑱输入'
',此时操作栈为NULL,直接入栈 ⑲输入'
',入栈 ⑳输入
,入栈 ㉑输入'
',优先级小于操作栈顶元素' ',入栈 ㉒输入'
',直接入栈 ㉓输入
,入栈 ㉔输入'
',优先级低于操作栈栈顶元素' ',入栈 ㉕输入
,入栈
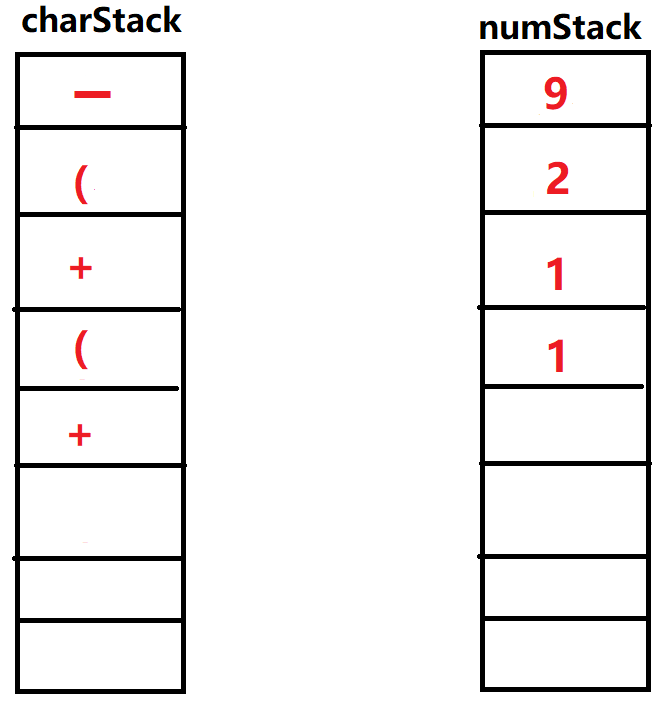
㉖输入'
',弹出操作符栈顶元素' ',弹出操作数栈两个元素 ,运算 。得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
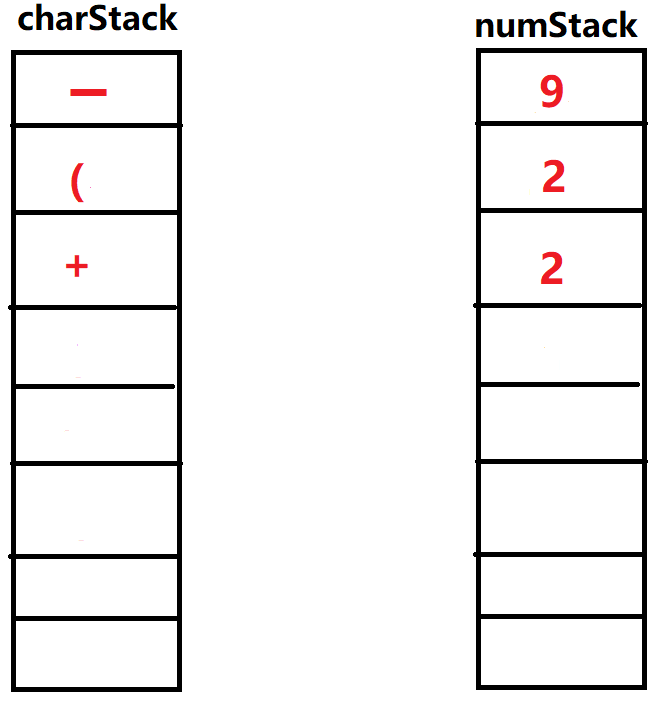
㉗输入'
',弹出操作符栈顶元素' ',弹出操作数栈两个元素 ,运算 。得到新的数字重新放回操作栈顶部,再次执行弹出元素为' ',这次运算结束。
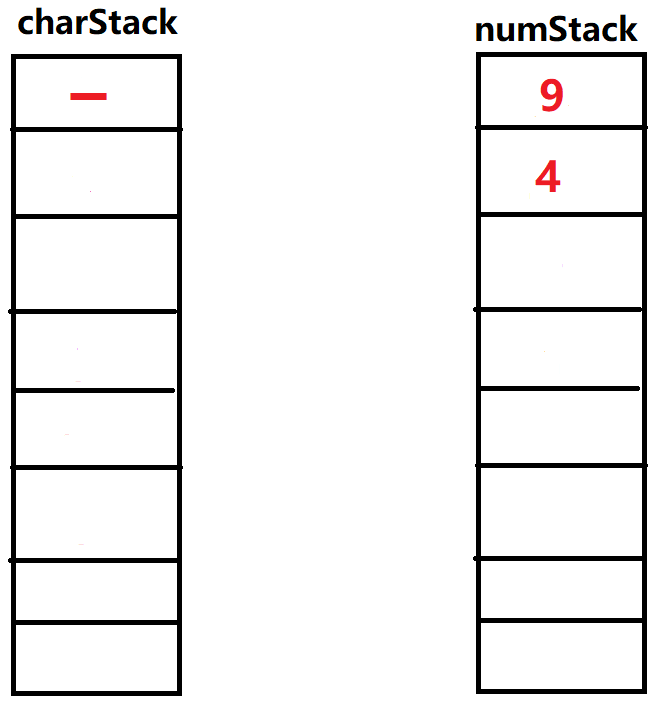
㉘弹出操作栈顶元素'
',弹出操作数栈两个元素进行最后运算,得到结果为
详细代码
xxxxxxxxxx2121using namespace std;5
6char arrGrad(char s){7 switch(s){8 case '+':9 return 'A';10 case '-':11 return 'A';12 case '*':13 return 'B';14 case '/':15 return 'B';16 default :17 return 'C'; 18 }19}20
21//存放运算符 22typedef struct linkC{23 char data;24 char grad; 25 struct linkC *next; 26} *linkChar;27
28//存放运算数 29typedef struct linkN{30 int data; 31 struct linkN *next; 32} *linkNum; 33
34bool initCharNum(linkChar &c,linkNum &n,char (&s)[MaxSize]){35 memset(s,'\0',sizeof(s));36 c=(linkChar)malloc(sizeof(linkChar));37 n=(linkNum)malloc(sizeof(linkNum));38 if(c==NULL||n==NULL) return false;39 c->next=NULL;40 n->next=NULL;41 return true;42}43
44//操作符入栈 45bool pushChar(linkChar &c,char s){46 linkChar p;47 p=(linkChar)malloc(sizeof(linkChar));48 if(p==NULL) return false;49 if(s=='+'|s=='-'){50 p->data=s;51 p->grad=arrGrad(s);52 p->next=c->next;53 c->next=p;54 return true;55 }else if(s=='*'|s=='/'){56 p->data=s;57 p->grad=arrGrad(s);58 p->next=c->next;59 c->next=p;60 return true;61 }else if(s=='('){62 p->data=s;63 p->grad=arrGrad(s);64 p->next=c->next;65 c->next=p;66 return true;67 }else{68 return false;69 } 70}71
72//操作数入栈 73bool pushNum(linkNum &n,int e){74 linkNum p;75 p=(linkNum)malloc(sizeof(linkNum));76 if(p==NULL) return false;77 p->data=e;78 p->next=n->next;79 n->next=p;80 81 return true;82}83
84//操作符出栈85char popChar(linkChar &c){86 char s;87 linkChar p;88 if(c->next==NULL) return 'E';89 s=c->next->data;90 p=c->next;91 c->next=p->next;92 free(p);93 return s;94}95
96//操作数出栈97int popNum(linkNum &n){98 int i;99 linkNum p;100 if(n->next==NULL) return 0;101 i=n->next->data;102 p=n->next;103 n->next=p->next;104 free(p);105 return i;106}107
108//获取操作符栈顶元素109char selectChar(linkChar &c,int e){110 if(e) return c->next->data;111 return c->next->grad;112}113
114//运算115void ope(linkChar &c,linkNum &n){116 char popchar=popChar(c);117 int num1=popNum(n);118 int num2=popNum(n);119 cout<<num2<<popchar<<num1<<endl;120 switch(popchar){121 case '+':122 pushNum(n,num2+num1);123 break;124 case '-':125 pushNum(n,num2-num1);126 break;127 case '*':128 pushNum(n,num2*num1);129 break;130 case '/':131 pushNum(n,num2/num1);132 break;133 }134} 135
136void printStack(linkChar &c,linkNum &n){137 while(c->next!=NULL){138 cout<<"data:"<<c->next->data<<"grad::"<<c->next->grad<<endl;139 c=c->next;140 }141 while(n->next!=NULL){142 cout<<"result:"<<n->next->data<<endl;143 n=n->next;144 }145}146
147//字符转数字 148int opeNum(char (&s)[MaxSize]){149 int couts,sum=0;150 for(int i=0;i<strlen(s);i++){151 couts=s[i]-'0';152 for(int j=i;j<strlen(s)-1;j++){153 couts=couts*10;154 }155 sum+=couts;156 }157 memset(s,'\0',sizeof(s));158 return sum;159}160int con=0;161
162//区分操作数和操作符163bool isCharNum(linkChar &c,linkNum &n,char s,char (&chrs)[MaxSize]){164 int i;165 if(s>='0'&&s<='9'){ //数字直接存入操作数栈 166 chrs[con++]=s;167 return true;168 }else if(s=='+'||s=='-'||s=='*'||s=='/'||s=='('||s=='!'){ //判断是否是操作符 169 if(strlen(chrs)>0) {170 i=opeNum(chrs);171 pushNum(n,i);172 con=0;173 }174 if(c->next==NULL){ //操作符栈为空,直接入栈 175 pushChar(c,s);176 return true;177 }178 if(selectChar(c,0)>=arrGrad(s)&&selectChar(c,1)!='('){ //不为空且栈顶操作符优先级大于等于当前所输入操作符元素,并且不是"("179 while(c->next!=NULL&&c->next->grad>=arrGrad(s)&&c->next->data!='('){ //取出操作符进行运算操作 180 ope(c,n);181 } 182 } 183 pushChar(c,s); //将当前输入操作符压入栈顶 184 return true;185 }else if(s==')'){ 186 if(strlen(chrs)>0||s=='!') {187 i=opeNum(chrs);188 pushNum(n,i);189 con=0;190 } //如果当前输入是")",弹出所有操作符进行运算,直到碰到"(" 191 while(selectChar(c,1)!='('){192 ope(c,n);193 }194 popChar(c); //弹出栈顶的"(" 195 return true;196 }else{197 return false;198 }199} 200
201int main(){202 char chr,chrs[MaxSize];203 linkChar c;204 linkNum n;205 initCharNum(c,n,chrs);206 while(chr!='!'){207 cin>>chr;208 isCharNum(c,n,chr,chrs);209 }210 ope(c,n);211 printStack(c,n);212} 5. 栈在递归中的应用
先给出一段代码,看一下函数调用背后过程
xxxxxxxxxx161void main(){2 int a,b,c;3 func1(a,b);4 c=a+b;5 ...6}7void func1(int a,int b){8 int x;9 func2(x);10 x=x+10086;11 ...12}13void func2(int x){14 int m,n;15 ...16}主函数用执行第一句代码后会在栈中存放
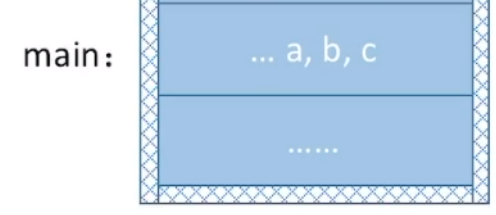
接着执行func1函数所对应代码,当执行func1时,会将后面应该执行代码,这里是表达式c=a+b地址同样压入栈中,图示如下(表达式地址用
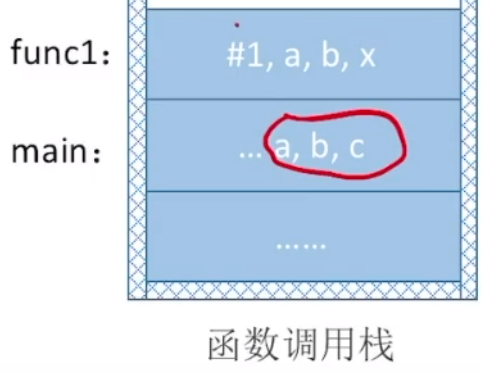
同样func2执行过程同上一步,表达式x=x+10086地址假设为
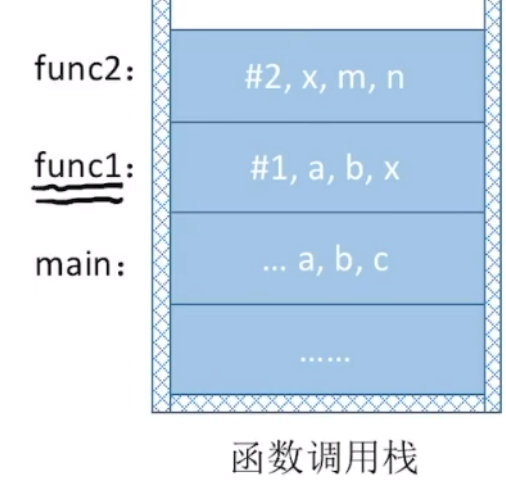
执行完func2函数后,之后弹栈,根据栈顶地址,执行c=a+b。
以上就是递归基本原理。适合用递归算法解决是:可以把原始问题转换为属性相同,但规模较小的问题。
实现递归两个重要条件:递归表达式,递归边界条件。

上面代码当执行到第10层时,2*1;之后以此类推。
上面也可以看出递归缺点就是非常占用栈空间,所以太多层递归可能会导致栈溢出。
五. 队列
队列是只允许在队尾一端插入(入队),在队头一端删除(出队)的数据结构。
特点:先进入先出(FIFO)。
栈的基本操作:创建、销毁、增加、删除、查询、判空。
1. 队列的顺序实现
1.1 队列初始化
xxxxxxxxxx121typedef struct Linknode{2 int data[MaxSize]; //数据域3 int front,rear; //队头指针和队尾指针 4 int size; //记录队列大小5} sqQueue; //队列 6
7//初始化8bool initQueue(sqQueue &s){9 s.front=0;10 s.rear=0;11 s.size=0;12} 1.2 入列
xxxxxxxxxx81//入列 2bool insertQueue(sqQueue &s,int e){3 if(s.size==MaxSize-1) return false; //判断队列是否已满4 s.data[s.rear]=e; //值赋给尾指针所指向的位置5 s.rear=(s.rear+1)%MaxSize; //尾指针+1取余变为循环队列6 s.size+=1; //队列元素个数+17 return true;8} 上面第五行取余操作,可以将对列变为循环队列。
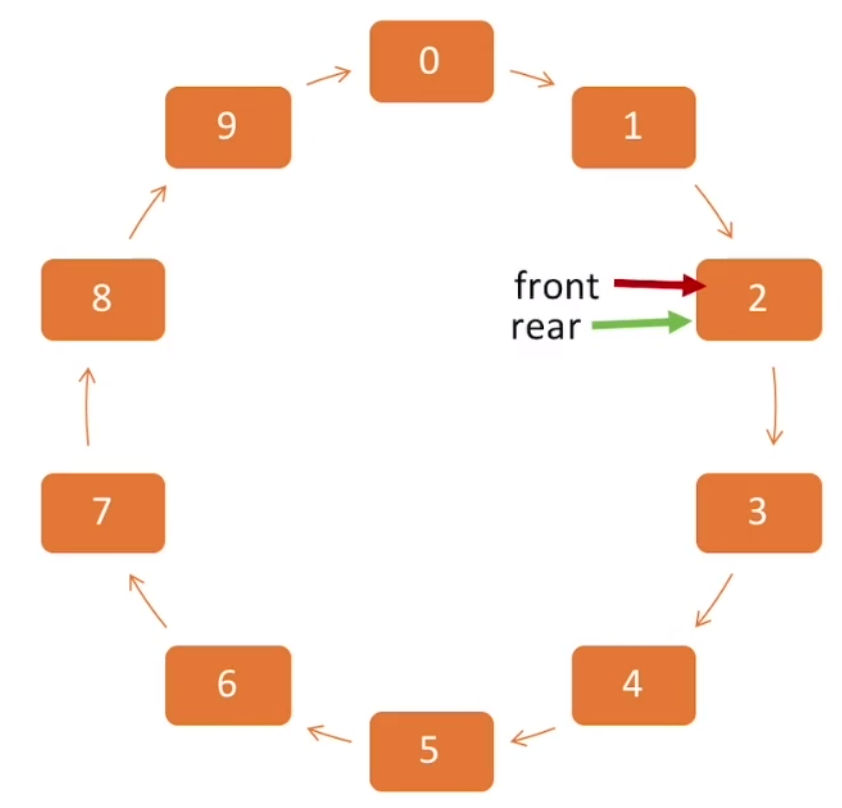
1.3 出列
xxxxxxxxxx81//出列 2bool popQueue(sqQueue &s,int &e){3 if(s.size==0) return false; //判断队列是否为空4 e=s.data[s.front]; //将头指针指向值赋值给e5 s.front=(s.front+1)%MaxSize; //头指针往后移一位,取余变为循环队列6 s.size-=1; //队列元素个数-17 return true;8} 和上面入列一样,这一队列变为循环队列,存储数据和读取数据更为方便。
1.4 队列元素个数
xxxxxxxxxx41//元素个数2void printQueue(sqQueue s){3 cout<<(s.rear-s.front+MaxSize)%MaxSize<<endl;4} 执行上面代码会实现当前队列中的元素个数。同时队列s.size中保存的也是元素个数。即
(s.rear-s.front+MaxSize)%MaxSize<<endl~s.size
1.5 其他情况
上面的都是队头队尾指针初始化时,指向同一位置,但有时候会碰见队尾指针在队尾情况
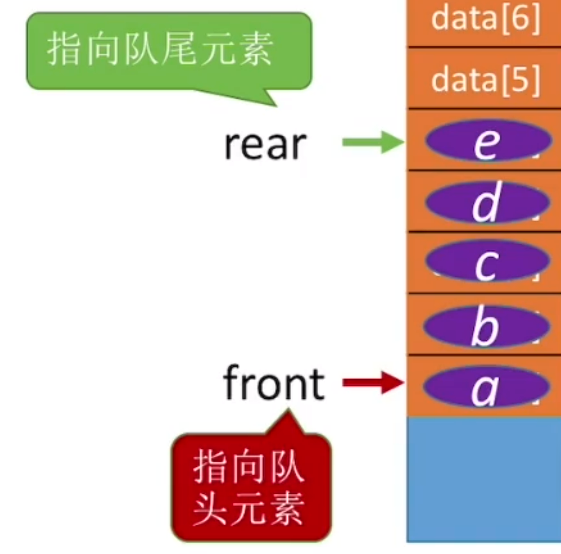
此时入队操作有所改变,我们要先让尾指针向后移一位,再进行插入。
xxxxxxxxxx61//入列 2bool insertQueue(sqQueue &s,int e){3 s.rear=(s.rear+1)%MaxSize; //尾指针+1取余变为循环队列4 s.data[s.rear]=e; //值赋给尾指针所指向的位置 5 return true;6} 而初始化方式也有所不同,让尾指针指向队尾元素,当第一次入队时通过取余操作,往后移动到第一位。
xxxxxxxxxx51//初始化2bool initQueue(sqQueue &s){3 s.front=0;4 s.rear=MaxSize-1; //尾指针指向尾部5} 判空操作和判满操作也不同:
xxxxxxxxxx21//判空2(s.rear+1)%MaxSize==s.front;判满操作同上,除了size判满操作,我们也可以通过设置辅助遍历tag来记录上次是入队操作,还是出队操作。由于只有入队操作会让队满,而只有出队操作会让队空,所以当入队时设置tag=1,当出队时设置tag=0。
xxxxxxxxxx21//通过tag方式判断队列已满2if((s.rear+1)%MaxSize==s.front&&s.tag==1)2. 链式队列
2.1 链式队列的初始化
xxxxxxxxxx201typedef struct Linknode{ //结点 2 int data; 3 struct Linknode *next; 4}linknode; 5
6typedef struct linkQueue{ //链式队列 7 linknode* front; //头指针 8 linknode* rear; //尾指针 9}linkQueue;10
11//初始化12bool initQueue(linkQueue &q){13 //带头节点方式: 14 q.rear=(linknode* )malloc(sizeof(linknode));15 q.front=q.rear;16 q.front->next=NULL;17 //不带头结点方式:18 //q.front=NULL;19 //q.rear=NULL; 20} 初始化创造两个结构体,第一个是结点,第二个存储链队列地址。

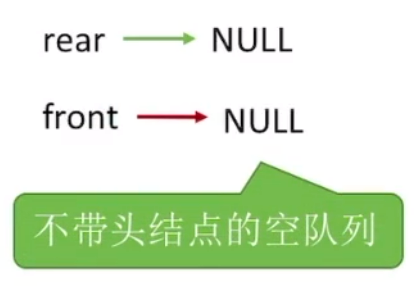
2.2 链式队列的入队
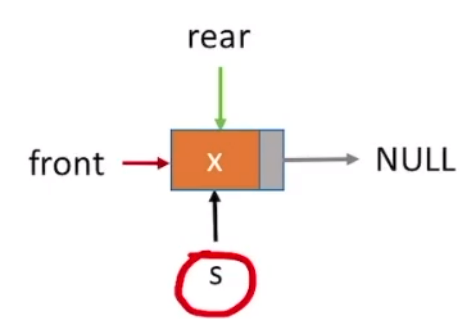
xxxxxxxxxx171//入队操作2bool insertQueue(linkQueue &q,int e){3 linknode *s=(linknode *)malloc(sizeof(linknode));4 s->data=e;5 s->next=NULL;6 //带头结点方式:7 //q.rear->next=s; //新结点插入到rear之后8 //q.rear=s; //修改表尾指针9 //不带头结点方式:10 if(q.front==NULL){ //条件成立,证明队列为NULL 11 q.front=s; //头指着指向s 12 q.rear=s; //尾指针指向s 13 } else{14 q.rear->next=s; //否则不为空,尾指针域指向s 15 q.rear=s; //尾指针指向s 16 }17} 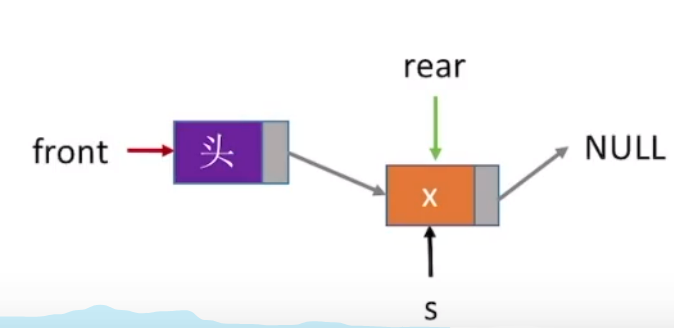
2.3 链式队列出队操作
带头结点出队
xxxxxxxxxx111//出队操作(带头结点)2bool DeQueue(linkQueue &q, int &e){3if(q.front==q.rear) return false; //空队4linknode *p=q.front->next;5e=p->data; //用变量e返回队头元素6q.front->next=p->next; //修改头结点的 next 指针7if(q.rear==p) //此次是最后一个结点出队8q.rear=q.front; //修改rear 指针9free(p); //释放结点空间10return true;11}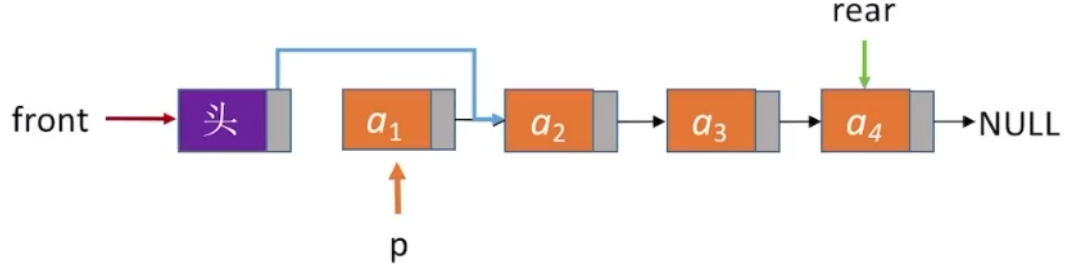
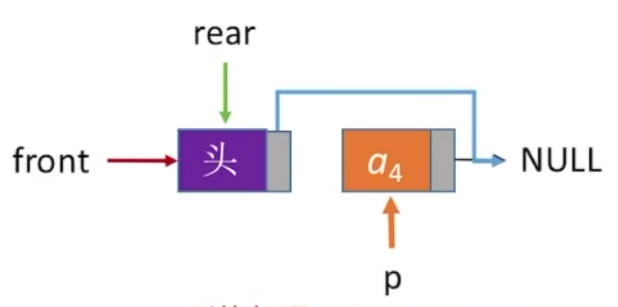
最后一个结点出队,实际上就是将队列再次变为空队列
不带头结点出队
xxxxxxxxxx131//不带头结点出队2bool DeQueue(linkQueue &q, int &e){3if(q.front==NULL ) return false; //空队4linknode *p=q.front; //p指向此次出队的结点5e=p->data; //用变量x返回队头元素6q.front=p->next; //修改front 指针7if(q.rear==p){ //此次是最后一个结点出队8q.front = NULL; //front指向NULL9q.rear = NULL; //rear指向NULL10}11free(p); //释放结点空间12return true;13}
3. 双端队列

具体又可以细分为:输入受限的双端队列、输出受限的双端队列

考点:和栈一样会考某组数据出栈顺序是否合法。可以用卡特兰数计算出一组数据有多少种合法出战组合。
4. 队列的应用——树的遍历
队列有一个重要应用:树的层次遍历。
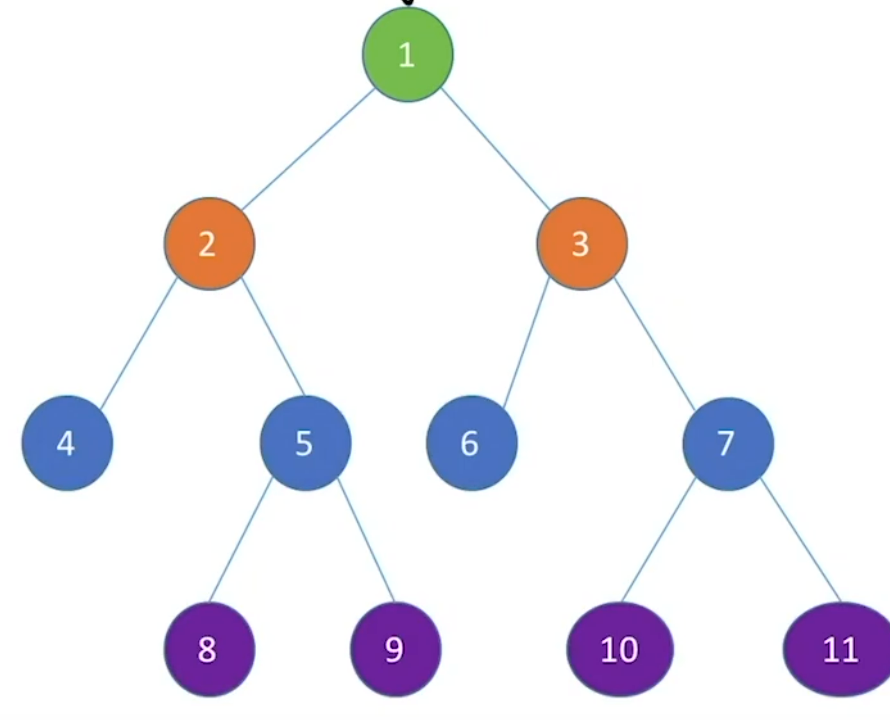
遍历步骤:
- 遍历
- 遍历完
- 遍历
- 之后遍历
- 遍历
- 遍历
- 遍历
- 依次遍历弹出即可
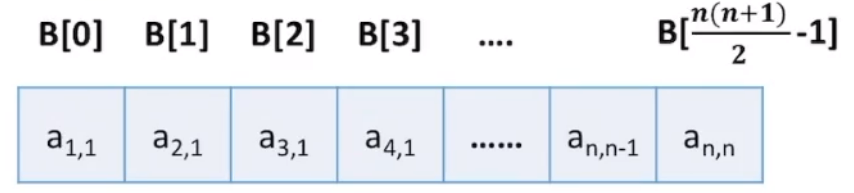
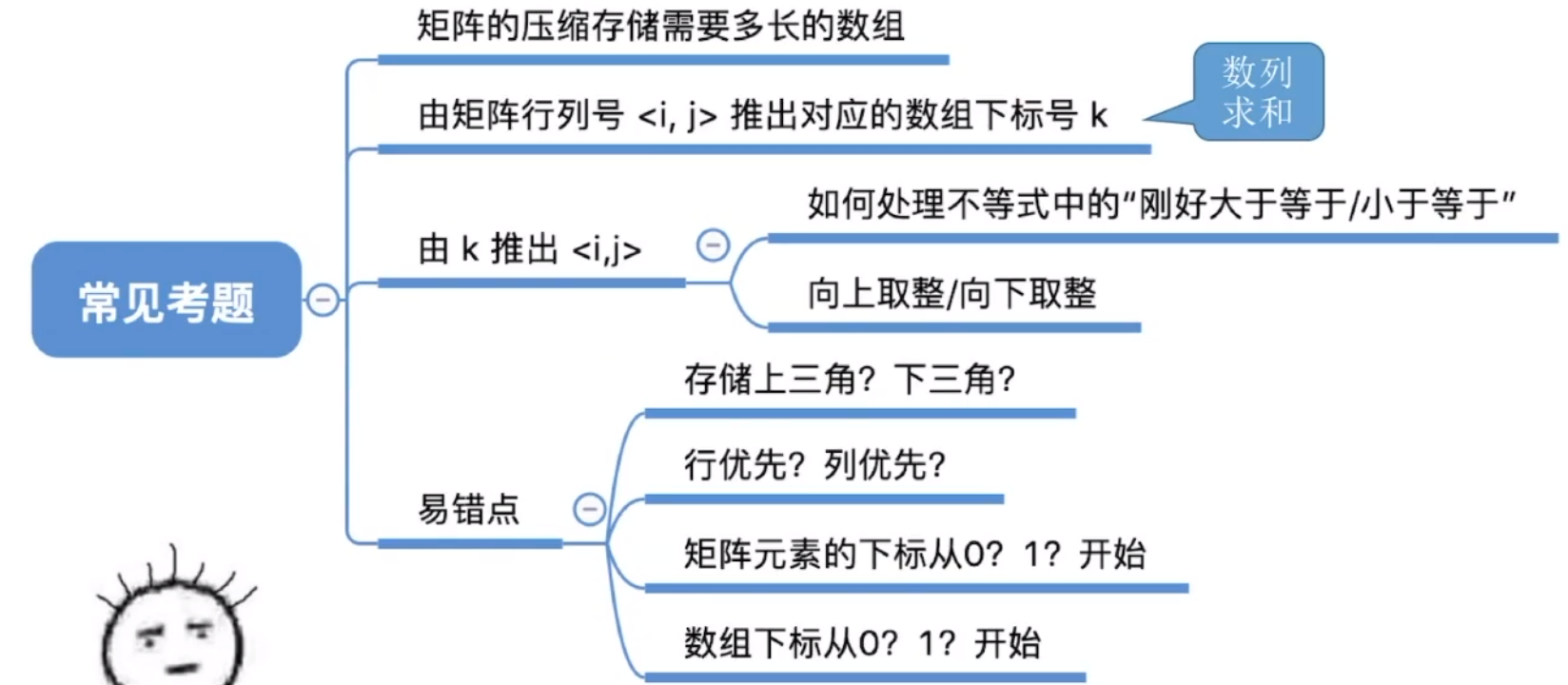
5. 特殊矩阵的压缩存储
5.1 一维数组
数组a[10]在内存中存储如下:

各个元素大小相同,且物理上连续存放。所以我们可以根据数组起始地址得到任何一个数组内存地址。
计算方法:i-1。
5.2 二维数组
数组b[2][4]内存存储如下:
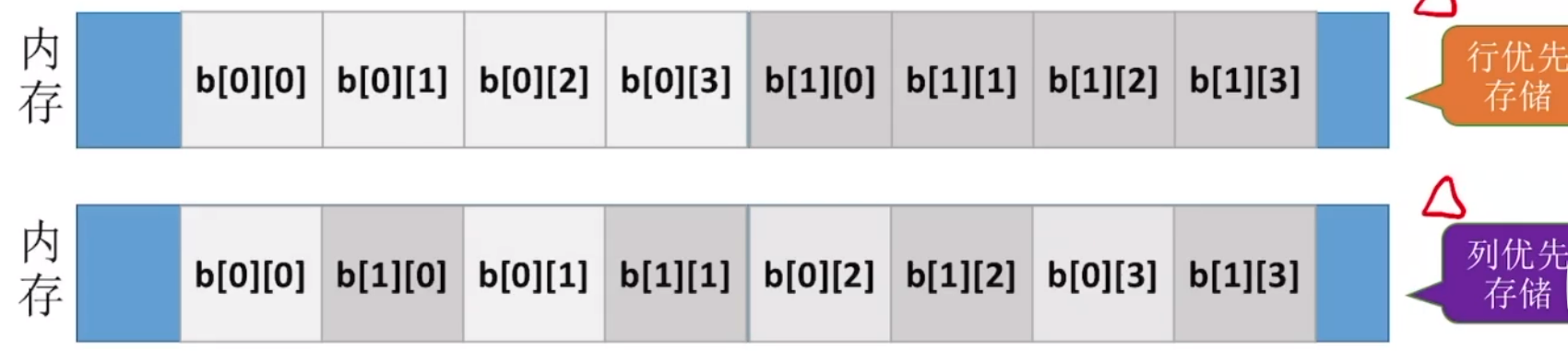
存储方式有两种:行优先(一行一行存),列优先(一列一列存)。
计算方法:b[m][n],按照行优先存储,则
b[m][n],按照列优先存储,则
5.3 对称矩阵压缩存储
若

其特点就是关于主对角线下标
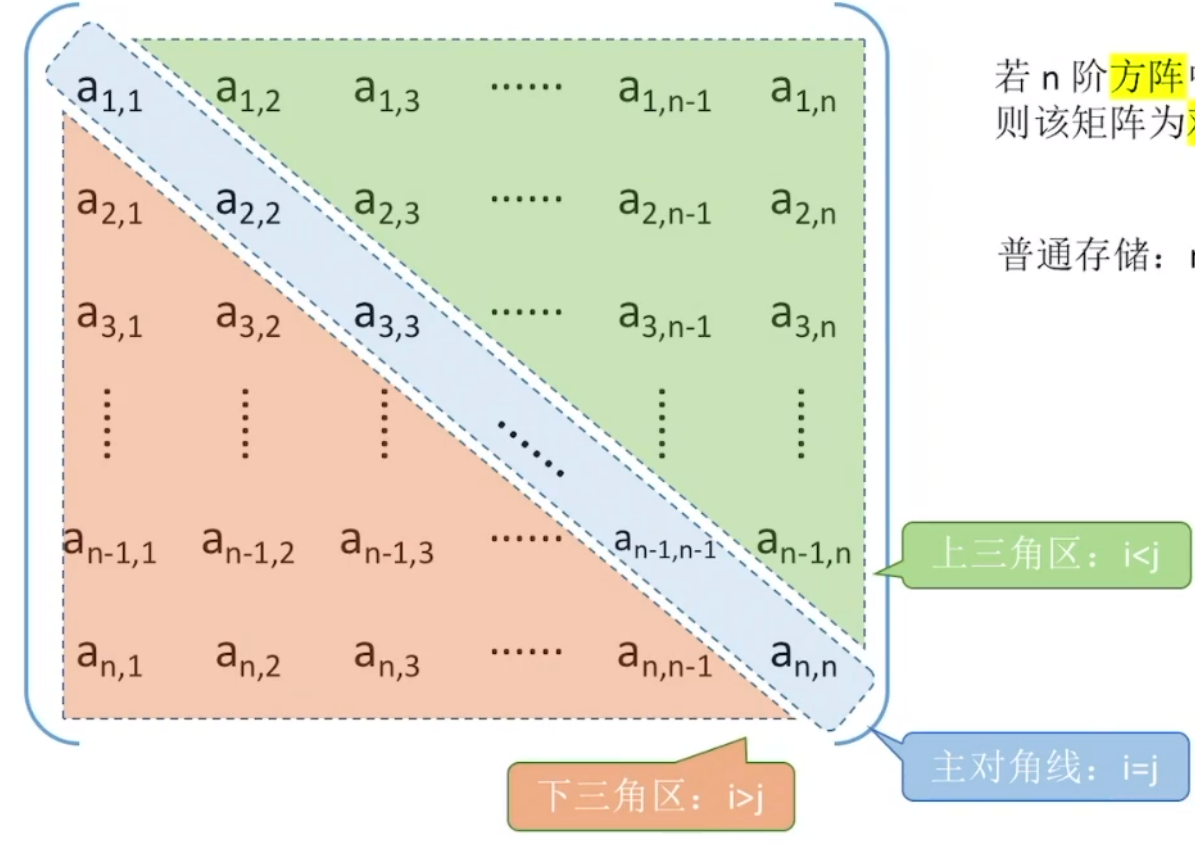
存储数组:数组从
存储方式:只存储主对角线
5.4 三角矩阵
下三角矩阵:除了主对角线和下三角区,其余的元素都相同
上三角矩阵:除了主对角线和上三角区,其余的元素都相同

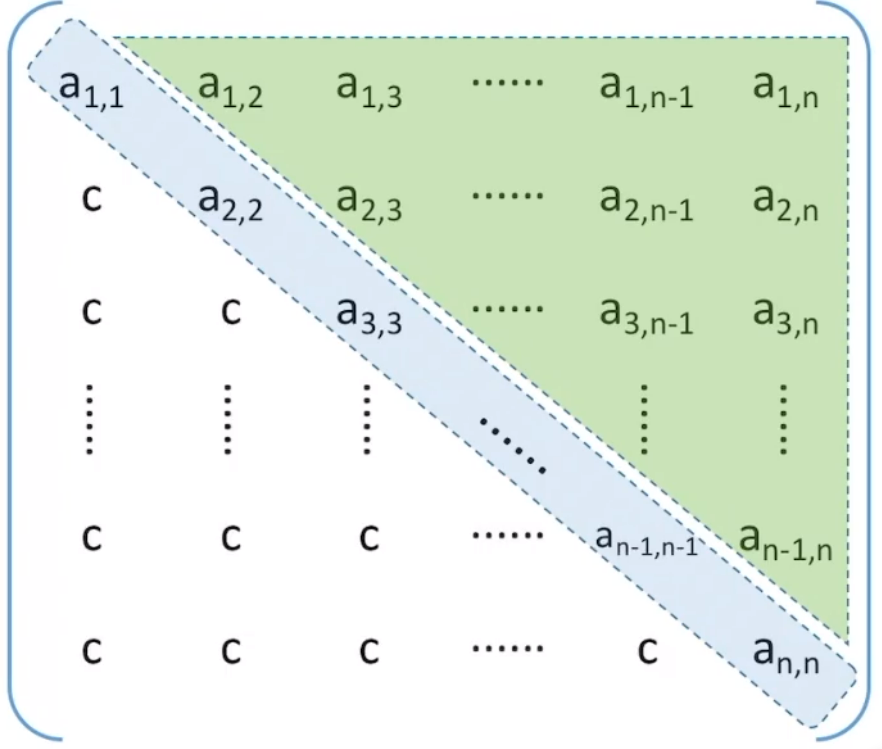
存储策略:按行优先原则将橙色区元素存入一维数组,并在最后一个位置存储常数

求
5.5 三对角矩阵的压缩存储
又称为带状矩阵,当满足
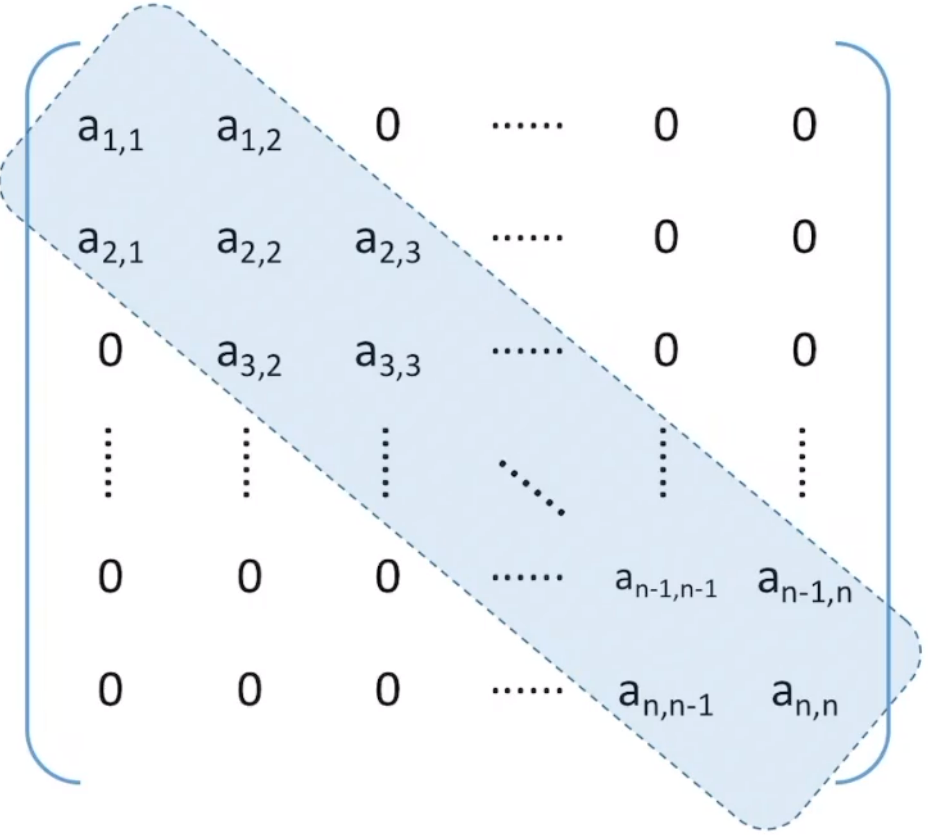
压缩策略:按行优先原则(列优先),只存储带状部分(非
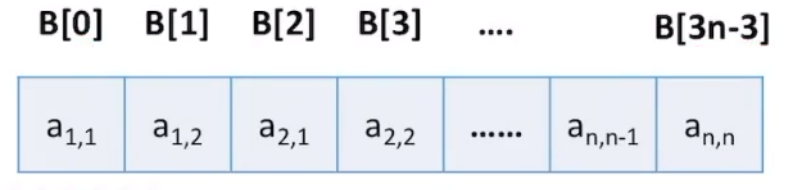
前
若已知数组下标
①前
②前
③显然
5.6 稀疏矩阵压缩存储
稀疏矩阵:非零元素远远少于矩阵元素个数。

压缩存储策略:
顺序存储:三元组,存储行、列、值
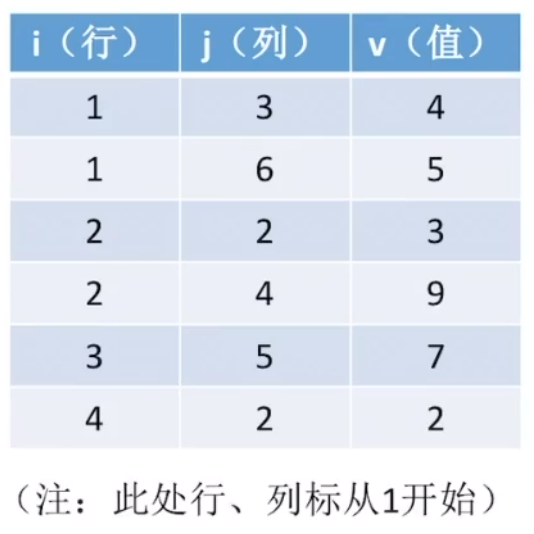
十字链表法:
定义一个节点,节点包含非零元素所在的行、列、值。节点还会有两个指针:
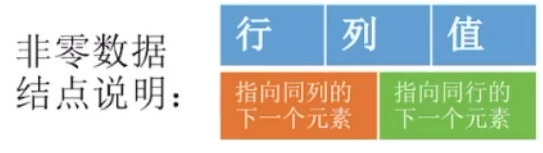
再定义两个数组:向下域(存放列指针)和向右域(存放行指针),数组中存放的是一个个指针。
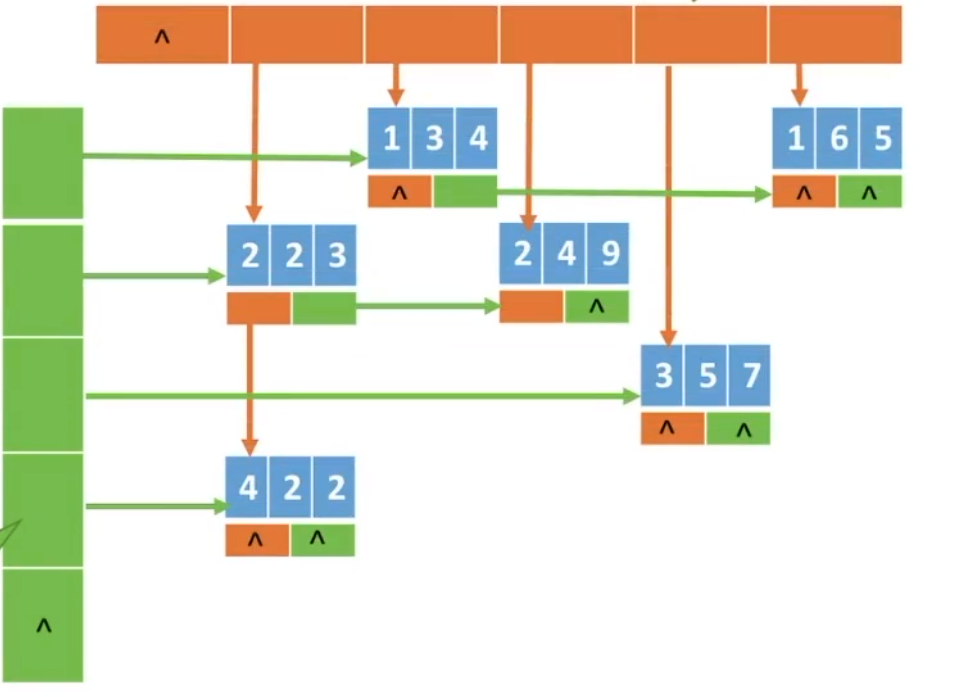
这里以行遍历为例:行数组中第一个指针指向节点值是4,其节点行指针域保存本行下一个非零元素指针,当找到下一个节点行指针域为NULL时。行数组
列遍历同行遍历。
六. 串
串,即字符串。是一种特殊的线性表,数据元素之间呈线性关系。
术语:
- 子串:串中任意个连续的字符组成的子序列。空串也是字符串的子串。
- 主串:整个字符串
- 字符在主串中的位置:字符在串中的序号,从
- 字串在主串中的位置:字串的第一个字符在主串中的位置,也是从
iPhone pro Max,pro在 - 只有长度为
串的基本操作增删改查等,通常以子串为操作对象。
字符集编码:任何数据存到计算机中一定是二进制数,需要确定一个字符和二进制数的对应规则,这就是"编码"。一般考试用ASCII编码,一个字符大小为
1. 串的存储方法
一般采用以下几种存储方法:

方案一缺点是从char[0]大小不能超过255。所以经常采用方案四。
2. 串的顺序存储
2.1 定长顺序存储
可以采用静态数组方式实现串的顺序存储
xxxxxxxxxx51typedef struct{3 char ch[MaxLEN];4 int length;5}SString;这样做缺点是数组长度是定长的,不能改变。
2.2 堆分配存储
用动态数组方式实现
xxxxxxxxxx61typedef struct{2 char *ch;3 int length;4}HString;5HString S;6s.ch=(char*)malloc(MaxLEN*sizeof(char));3. 串的链式存储
3.1 低密度存储
存储密度低,每个字符
xxxxxxxxxx41typedef struct StringNode{2 char ch;3 struct StringNode *next;4}StringNode,*String;
3.2 高密度存储
每个结构体有一个长度为
xxxxxxxxxx41typedef struct StingNode{2 char ch[4];3 struct StingNode *next;4}StingNode,*String;
最后一个节点存储不满,可以用特殊字符标记,建议用\0
4. 字符串基本操作
4.1 求字串
要求:用sub返回串S的第pos个字符起长度为len的子串。
xxxxxxxxxx121typedef struct{2 char ch[MaxLEN];3 int length;4}SString;5bool SubString(SString &Sub,SString S,int pos,int len){//sub:暂存;S:主串;pos:起始位置;len:截取长度6 if(pos+len-1>S.length) return false; 7 for(int i=pos;i<pos+len;i++){8 Sub.ch[i-pos+1]=S.ch[i];9 }10 Sub.length=len;11 return true;12}4.2 字符串比较
若
xxxxxxxxxx71int StrCompare(SString S,SString T){2 for(int i=1;i<=S.length&&i<=T.length;i++){3 if(S.ch[i]!=T.ch[i]) return S.ch[i]-T.ch[i];4 }5 //所有字符串都相同,则长度大的字符串大6 return S.length-T.length;7}4.3 定位操作
若主串
xxxxxxxxxx101int Index(SString S,SString T){2 int i=1,n=StrLength(S),m=StrLength(T);3 SString sub;//暂存字串4 while(i<=n-m+1){5 SubString(sub,S,i,m);6 if(StrCompare(sub,T)!=0) ++i;7 else return i;//返回子串在主串中的位置8 }9 return 0;10}每次从
5. 朴素模式匹配算法
字符串模式匹配:在一大片字符串(主串)中搜索某个字符串(模式串)。如:一个文档中搜索一段话。
这里解释较容易混淆概念:子串是主串的一部分,一定存在。模式串不一定能在主串中找到。
朴素模式匹配思路:在主串中依次取和模式串长度相同字符串进行匹配。如:主串长度为
代码实现:用两个标记指针
xxxxxxxxxx131int Index(SString S,SString T){2 int i=1,j=1;3 while(i<=S.length&&j<=T.length){4 if(S.ch[i]==T.ch[i]){5 ++i,++j;//字符相等继续比较后续字符6 }else{7 i=i-j+2;8 j=1//指针后退重新开始匹配9 }10 }11 if(j>T.length) return i-T.length;//返回主串中匹配相同位置12 else return 0;//所有都不匹配返回013}时间复杂度:最坏情况,每个子串都要对比
6. KMP算法匹配字符串
KMP算法是朴素模式匹配算法优化。利用好模式串本身带有的信息可以跳过中间很多没有必要的对比,从而使算法效率得到提升。给出一组子串和一个模式串:
从主串


对于模式串
T='abaabc',当第6个元素匹配失败时,可令主串指针

从主串


同样对于模式串
T='abaabc',当第6个元素匹配失败时,可令主串指针

从主串
T='abaabc',当第5个元素匹配失败时,也就代表主串中前四个元素信息可以确定是abaa。此时可以让主串指针

从主串
T='abaabc',当第4个元素匹配失败时,也就代表主串中前三个元素信息可以确定是aba。此时可以让主串指针

以此类推,主串
T='abaabc',当第3个元素匹配失败时,也就代表主串中前二个元素信息可以确定是ab。可以让主串指针

同样的假定模式串第
当第
优化后的主串指针T='abaabc',回溯有以下情况:

我们可以用一个

当第一个元素匹配失败时,令
判断代码:
xxxxxxxxxx71if(S[i]!=T[j]){2 j=next[i]3}4if(j==0){5 i++;6 j++;7}模式匹配部分完整代码:
xxxxxxxxxx131int Index_KMP(SString S,SString T,int next[]){2 int i=1, j=1;3 while( i<=S.length&&j<=T.length){4 if(j==0||S.ch[i]==T.ch[j]){5 ++i;6 ++j; //继续比较后继字符7 }8 else j=next[j]; //模式串向右移动9 }10 if(j>T.length)11 return i-T.length; //匹配成功12 eLse return 0;13}KMP算法最欢时间复杂度
7. 求next数组
求next数组过程很关键,要利用next数组进行匹配,主串指针不用回溯,从而减少时间复杂度。
求字符串google的next数组过程:字符串google长度是
此时让
next[1]都无脑写任何模式串都一样,第
next[2]都无脑写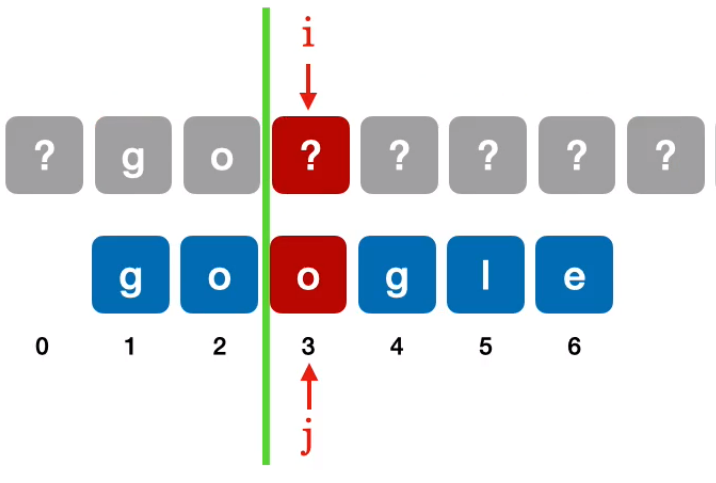
尝试模式串往后移动一位与主串对应元素进行匹配:
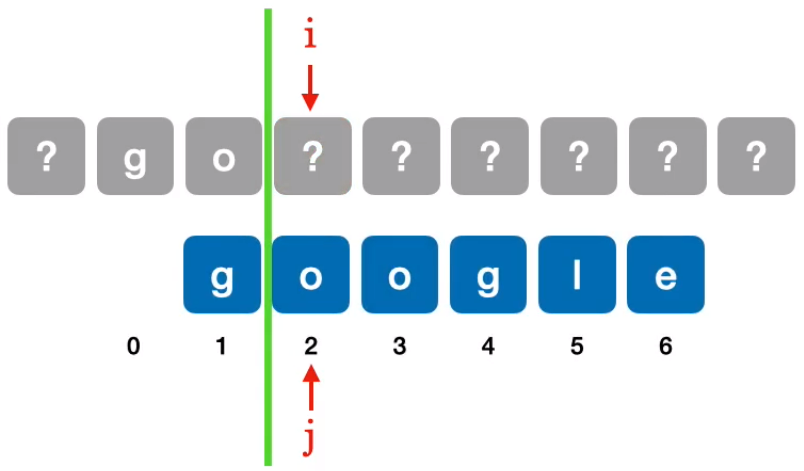
显然
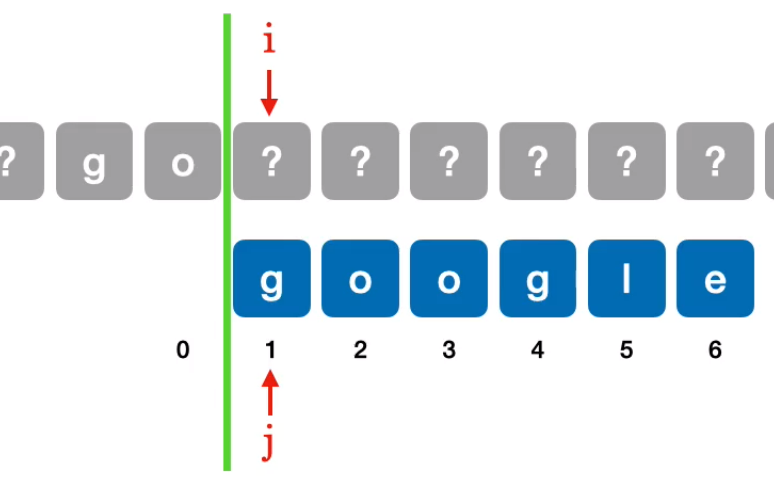
此时移动到匹配失败元素的位置,而指针
同理,当第四个元素匹配失败要回溯位置
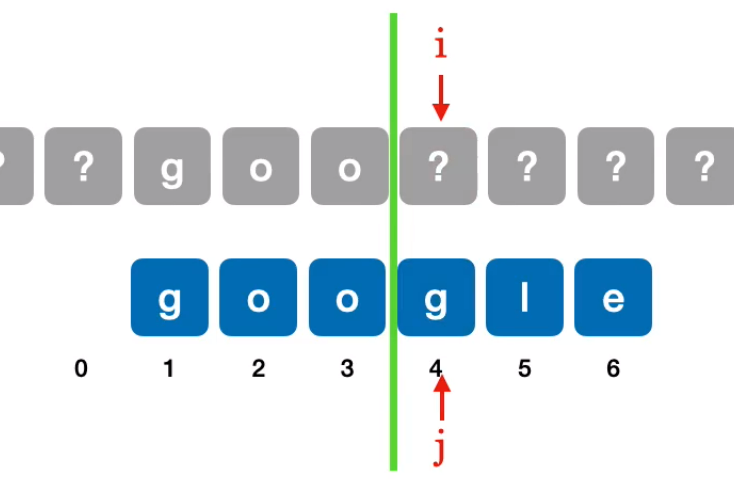
模式串右移一位,与对应主串匹配:
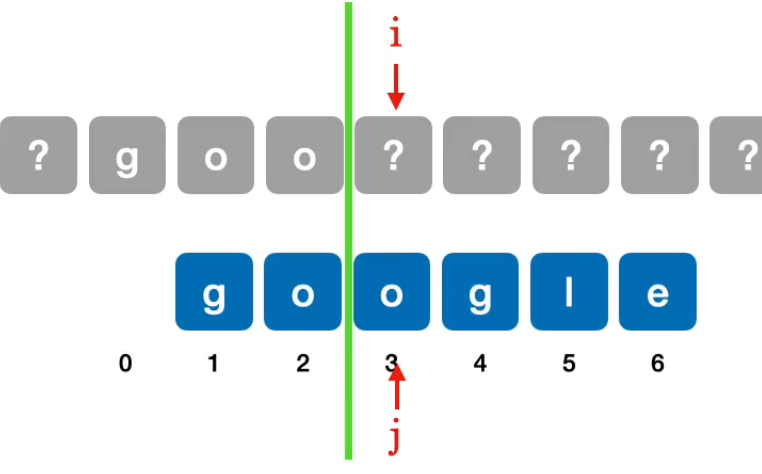
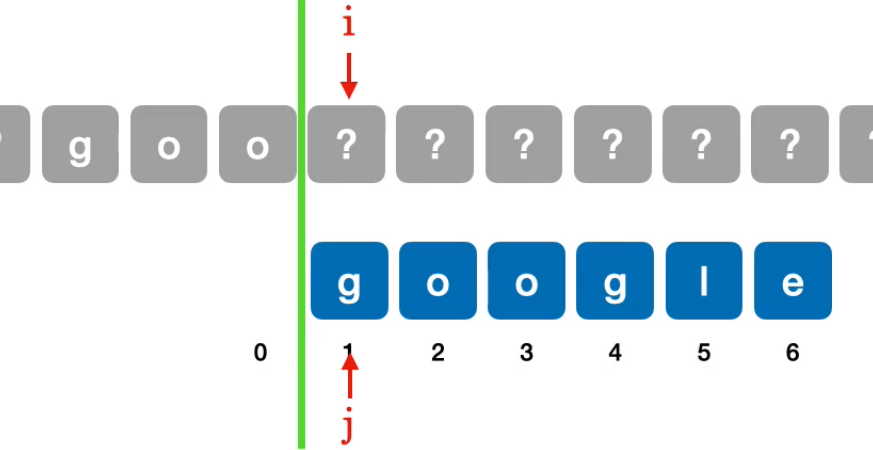
此时
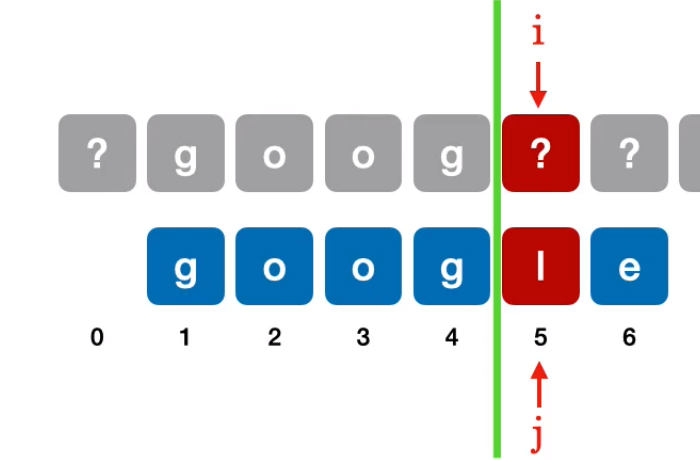
模式串右移同时观察是否匹配对应主串,当移动到第四位时:
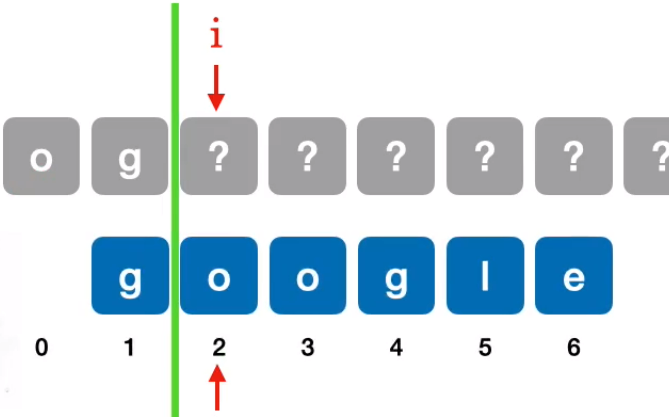
发现模式串第一位
next[5]=j,即next[5]=2同理得
总结:next数组的作用:当模式串的第j个字符失配时,从模式串的第next[j]的继续往后匹配
步骤总结:在不匹配的位置前边,划一根分界线,模式串一步一步往后退,直到分界线之前能匹配上,或模式串完全跨过分界线为止此时
xxxxxxxxxx231//计算next数组 2void nextVal(char s[],int next[],int len){3 //c是不匹配的位置,i主串位置,j匹配串位置;由于前两位匹配失败回溯值确定,所以从第三个位置开始匹配4 //由于不匹配位置从3开始,故主串自动右移一位与模式串第一位进行匹配,即i=2,j=15 int c=3,i=2,j=1;6 while(c<=len){7 //首次循环如果模式串第一位匹配主串第二位是否相等8 if(s[i]==s[j]){9 //如果相等主串与模式串指针继续后移匹配10 ++i,++j;11 }else{12 //如果不相等,主串继续后移,模式串回溯到1重新匹配13 i=i-j+2;14 j=1;15 }16 //如果主串指针i指向不匹配元素位置,则结束本次匹配,j的值就是next[c]的值17 if(i==c){18 next[c]=j;19 //继续计算下一次next[c]的值20 c++;21 }22 }23} 8. KMP算法进一步优化
本质是对next数组的优化,将next数组优化为nextval数组。
以模式串abaabc为例,其对应next数组如下:

当a,而回溯之前匹配失败位置a,所以主串所指位置a,这样又要将模式串进行
即

直接办法是让next[3]=next[1]=0,此时如果模式串第三个位置匹配失败,执行
同理,

其代码实现核心是失败位置
xxxxxxxxxx121//优化next数组,s模式串,len模式串长度2void nextVals(char s[],int next[],int nextVal[],int len){3 for(int i=2;i<=len;i++){4 if(s[next[i]]==s[i])5 nextVal[i]=nextVal[next[i]];6 else7 nextVal[i]=next[i];8 }9 for(int i=1;i<=len;i++){10 cout<<"nextVal:"<<nextVal[i]<<endl;11 }12} 七 树
树是一种递归定义的结构。树的结构如下:
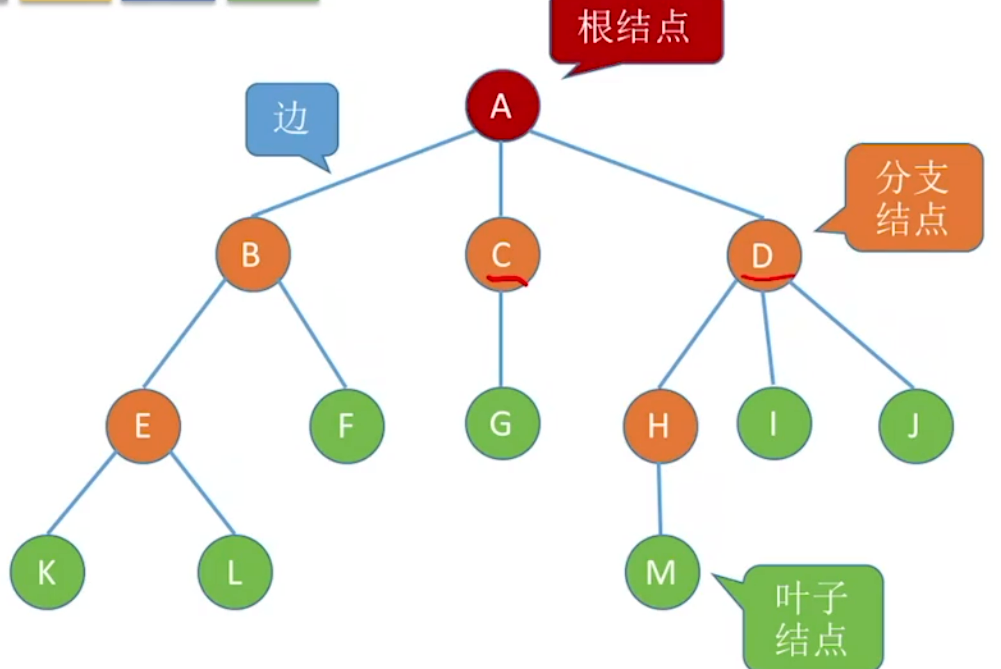
以上是非空树结构,还有空树
1. 树的基本概念
非空树特点:
有且仅有一个根节点
没有后继的结点称为"叶子结点"(或终端结点)
有后继的结点称为"分支结点"(或非终端结点)
除了根节点,任何一个节点都有且仅有一个前驱
每个节点可以有
除根节点外,其余节点可以分为若干个子树,这些子树特点是互不相交
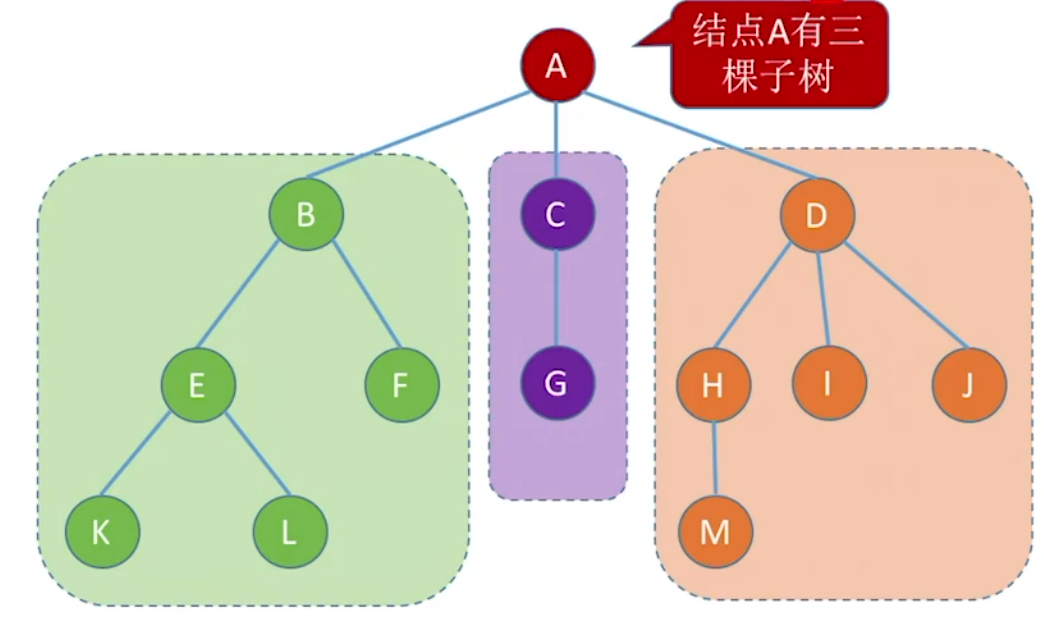
结点之间的关系描述:
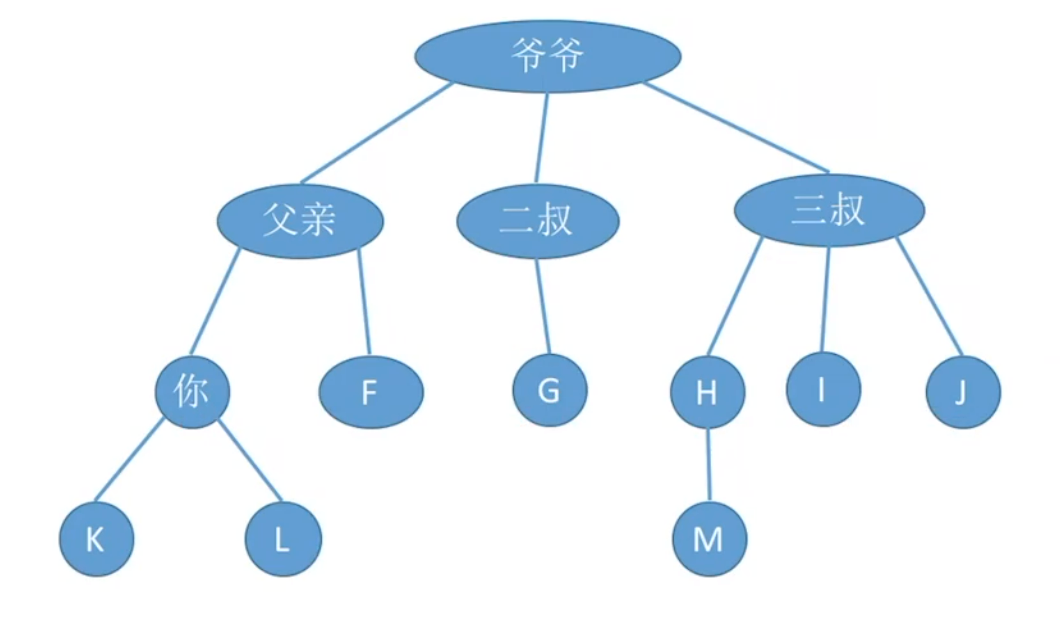
祖先结点:从子结点开始,往上经过结点都是祖先结点
如:
爷爷父亲是你的祖先结点孙子结点:从子结点开始,下面的分支都是孙子结点
如:
F是父亲的孙子结点双亲结点(父结点):一个结点直接前驱是父结点
如:
你的父结点是父亲孩子结点:一个结点的直接后继是孩子结点
如:
H的孩子结点是M兄弟结点:子树同一层结点为兄弟结点
如:
I,j是H的兄弟结点堂兄弟结点:同一层结点为堂兄弟结点
如:
G,H,I是J的堂兄弟结点路径:描述两个结点之间的路径,是单向的,只能从上往下。
路径长度:指经过了几条边
结点、树的属性描述
属性: 结点的层次(深度)——从上往下数

结点的高度——从下往上数

树的高度(深度)——树总共多少层
结点的度——一个结点有几个分支(包括根结点)。非叶子结点的度
树的度——各结点的度的最大值。如上面树的度D
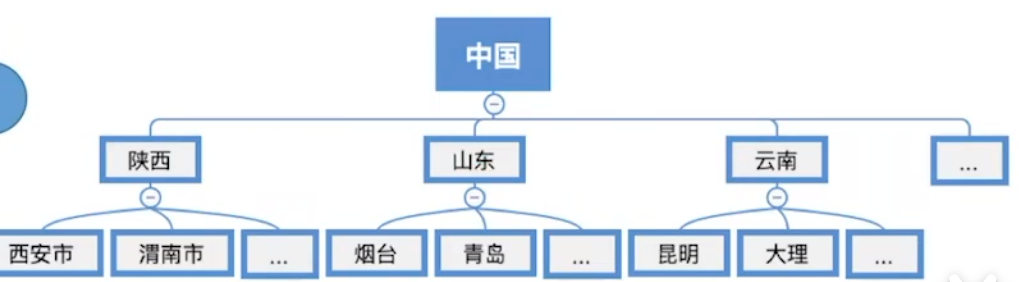
有序树:逻辑上看,树种结点的各子树从左到右是有次序的,不能互换。如:

无序树:树中结点的各子树从左至右是无次序的,可以互换。如:
森林:森林是
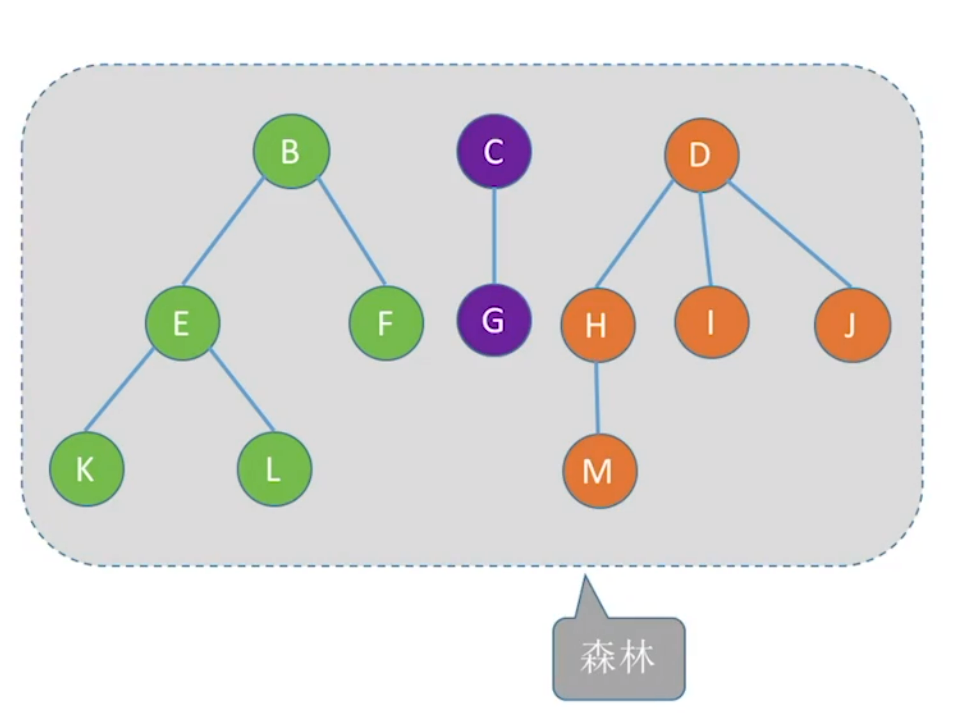
如果以上森林加一个共同根节点A,森林就变成了树。这是一个重要考点。
2. 树常考的性质
考点一:结点数
考点二:度为
度为 任意结点的度 任意结点的度 至少有一个结点度 允许所有结点的度都 一定是非空树,至少有 可以是空树 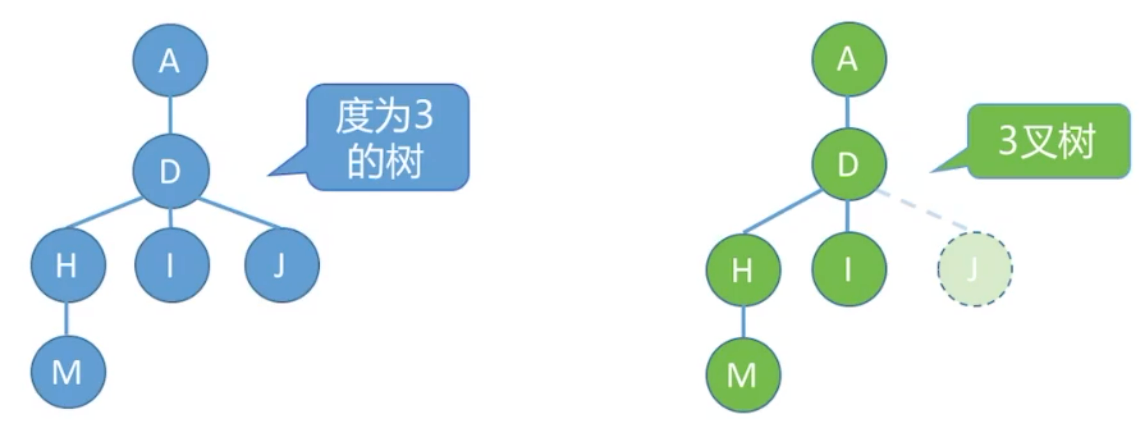
考点三:度为
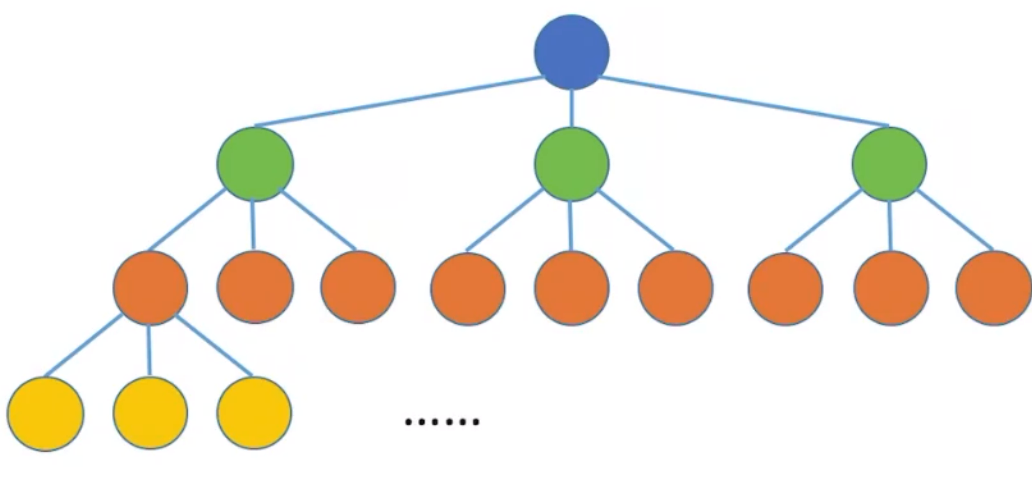
第一层:最多
同理,
考点四:高度为
考点五:高度为

考点六:具有
高度最小情况:所有结点都有
考点七:设非空二叉树中度为
假设树中结点总数为
①
②
此时②
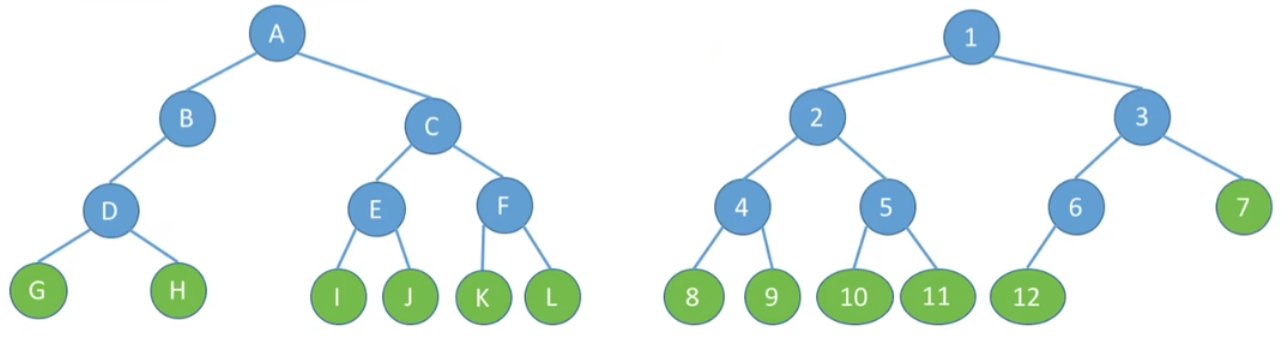
考点八:二叉树第
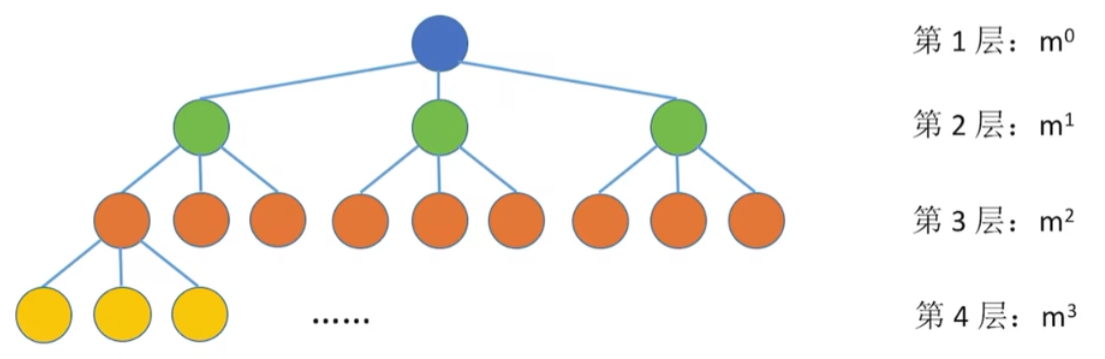
考点九:高度为
等比数列求和公式:
完全二叉树考点
高为
高为
故

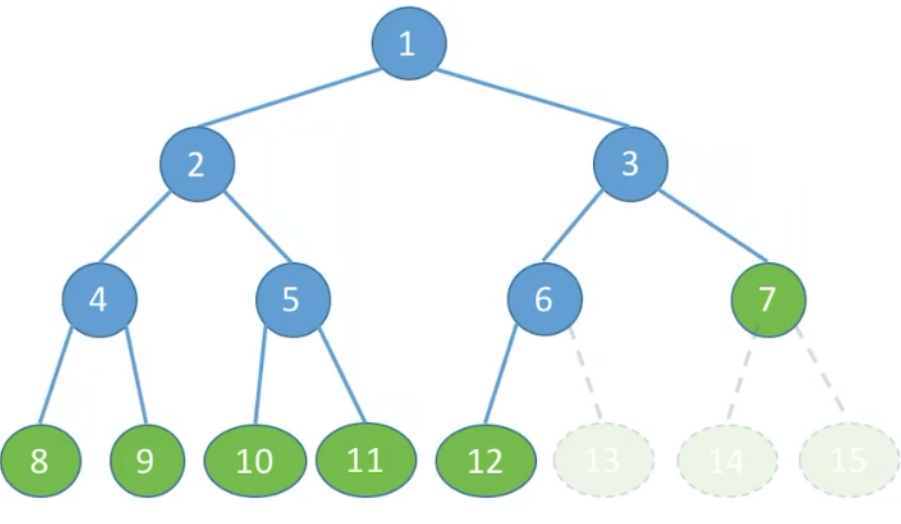
完全二叉树考点
完全二叉树最多只有一个度为
假设
例:若一个完全二叉树有

3. 二叉树
二叉树是
①或者是空二叉树,即
②或者由一个根结点和两个互不相交的被称为根的左子树喝右子树组成,左子树和右子树又分别是一颗二叉树。
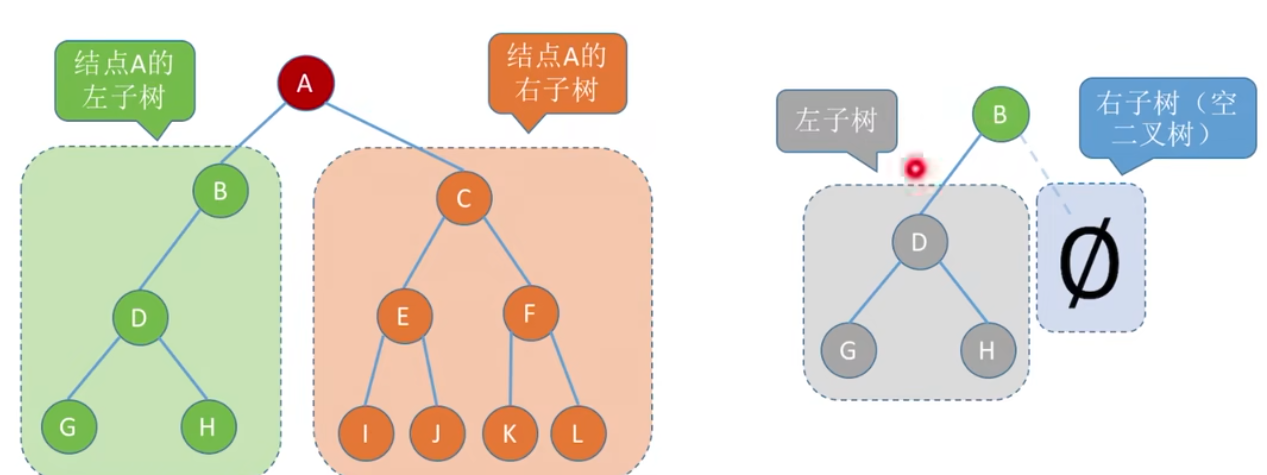
特点:每个结点至多只有两棵子树,左右子树不能颠倒(二叉树是有序树);二叉树是递归定义的数据结构。
二叉树五种状态:
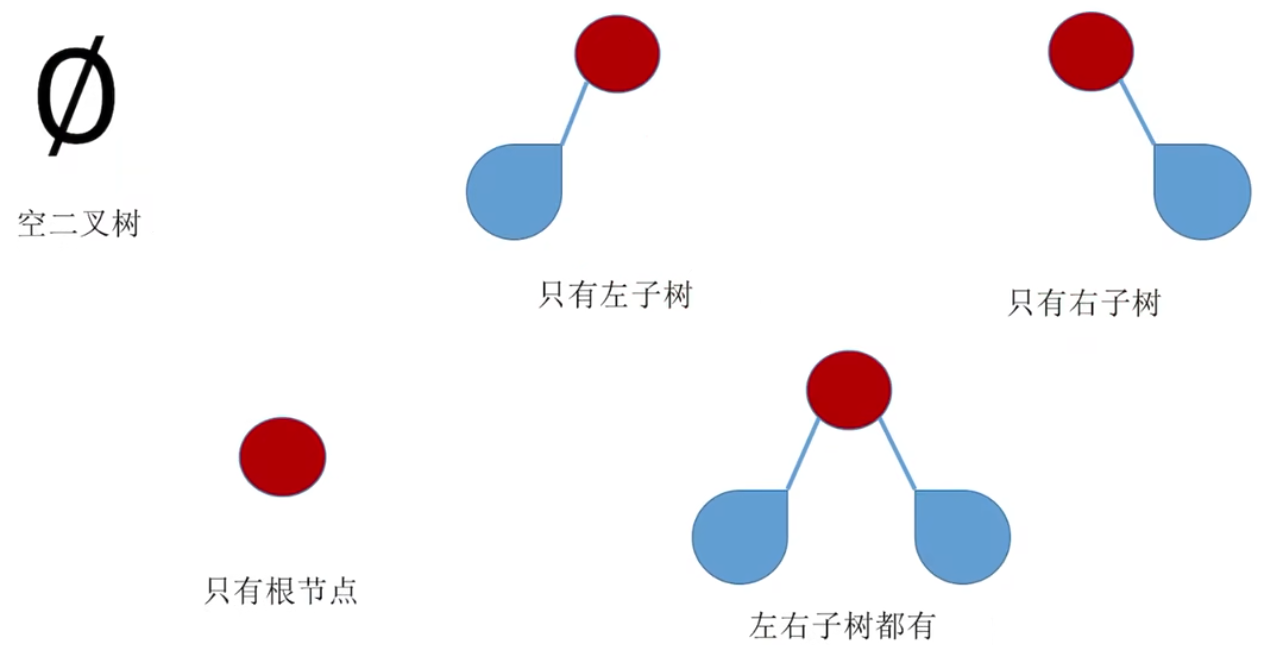
3.1 几个特殊二叉树
满二叉树
满二叉树:一棵高度为
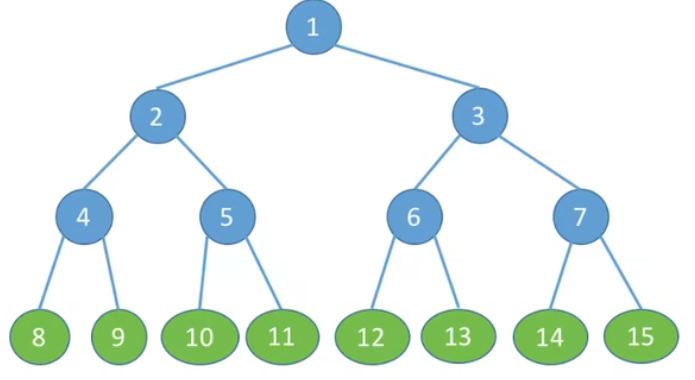
特点:
①只有最后一层有叶子结点;
②不存在度为
③按层序从
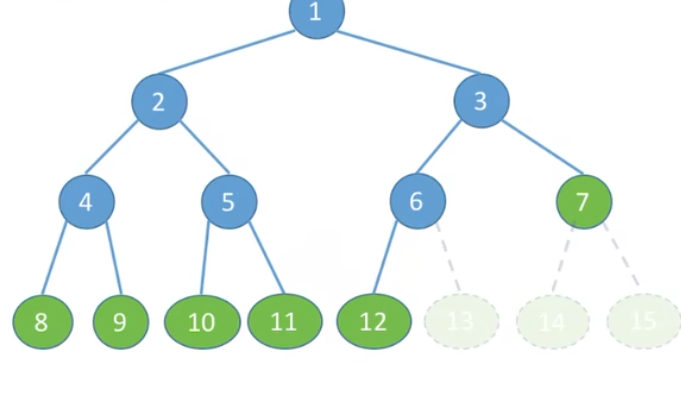
完全二叉树
完全二叉树:当且仅当其每个结点都与高度为
特点:
①只有最后两层可能有叶子结点;
②且最多只有一个度为
③按层序从
④
⑤一个结点如果有孩子,一定是左孩子。
满二叉树是完全二叉树,而完全二叉树不一定是满二叉树。
二叉排序树
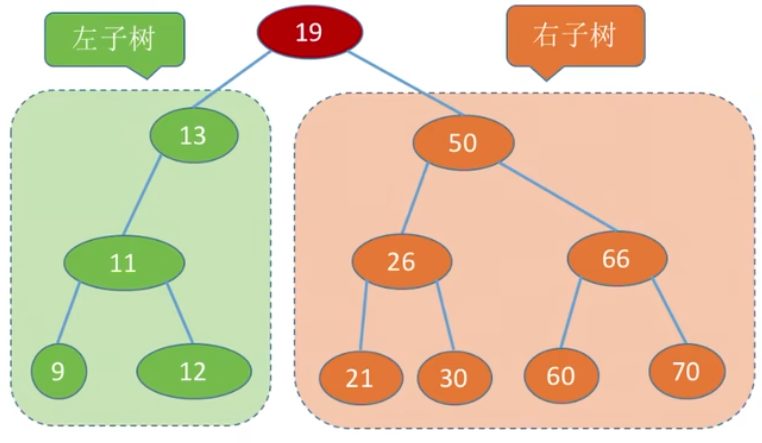
二叉排序树是一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树:
①左子树上所有结点的关键字均小于根结点的关键字;
②右子树上所有结点的关键字均大于根结点的关键字。
③左子树和右子树又各是一棵二叉排序树。
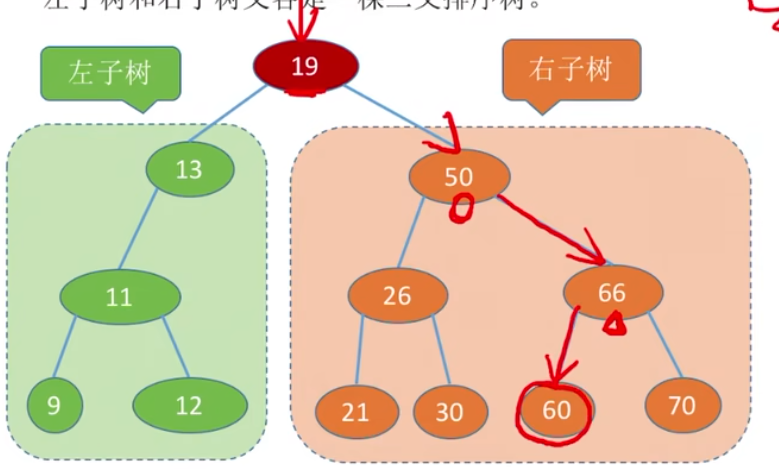
例:如果找60这个元素,先从根结点开始,根结点60元素的结点。
平衡二叉树
平衡二叉树,树上任一结点的左子树和右子树的深度之差不超过
特点是:根节点子树越多,高度越低,搜索排序的效率越高。

同样平衡二叉树排序搜索效率很高。
3.2 二叉树存顺序储结构
完全二叉树顺序存储
完全二叉树几个常考的基本操作:
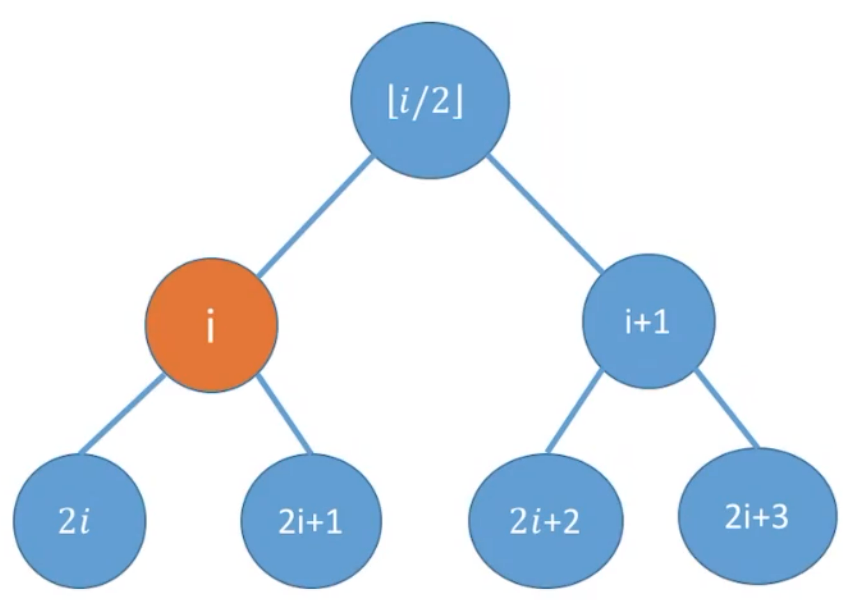
若完全二叉树中共有
- 判断
- 判断
- 判断
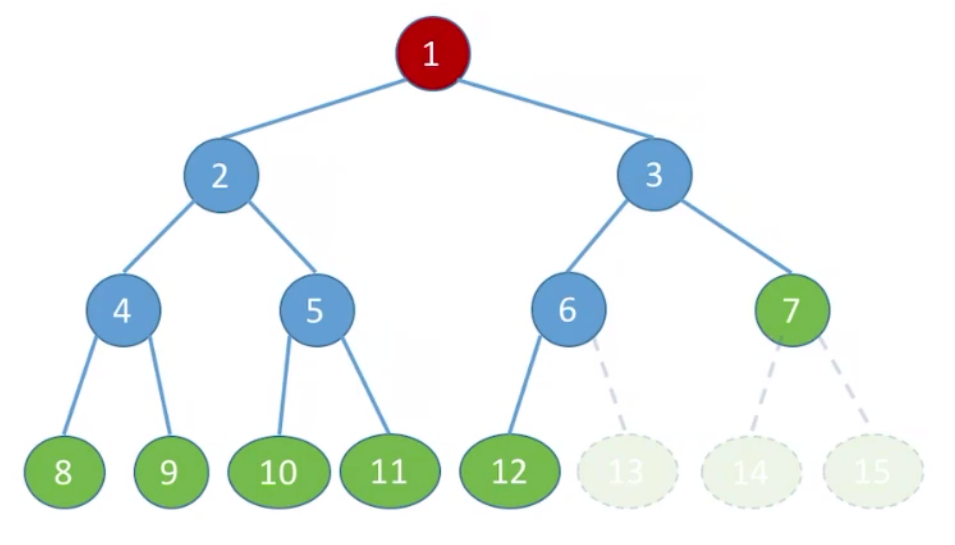
要存储下面完全二叉树结构:
xxxxxxxxxx221using namespace std;5
6struct treeNode{7 int data;8 bool isEmpy;9};10
11//初始化,所有结点标记为空12void initNode(treeNode t[]){13 for(int i=0;i<MaxSize;i++){14 t[i].isEmpy=true;15 }16}17
18
19int main(){20 treeNode t[MaxSize];21 initNode(t);22}这里结构体中的isEmpy变量是该结点有没有元素,有的话为false,初始化时默认为true。其树元素在顺序表中存储如下:

可以让第一个位置空缺,保证数组下标和结点编号一致。
非完全二叉树顺序存储
要存储下面二叉树结构:
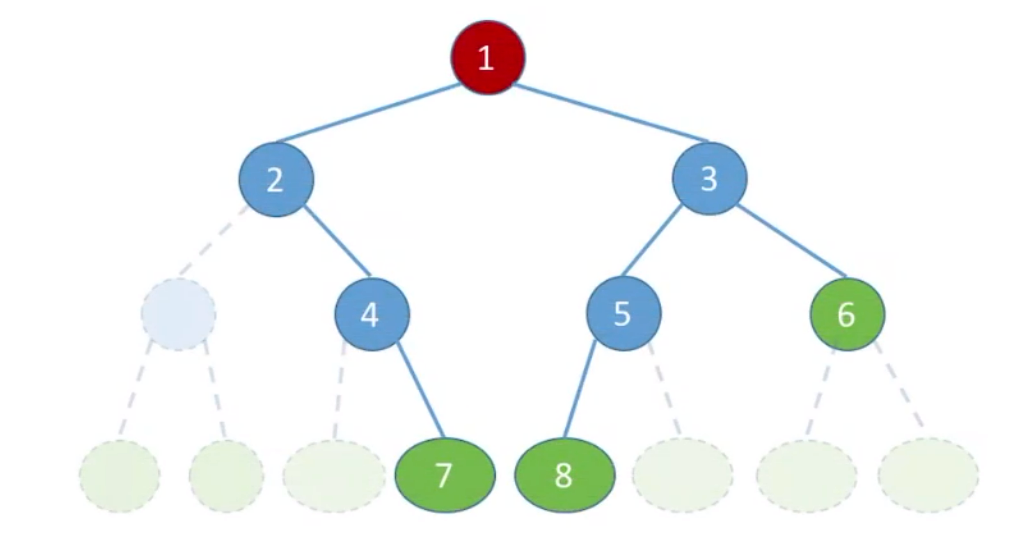
如果不是完全二叉树,依然按层序将各节点顺序存储,无法从结点编号反映出结点间的逻辑关系。

这种存储方法不能用完全二叉树操作解决,所以是错误的。
解决方法是将二叉树结点编号与完全二叉树对应起来。将二叉树重新编号如下:
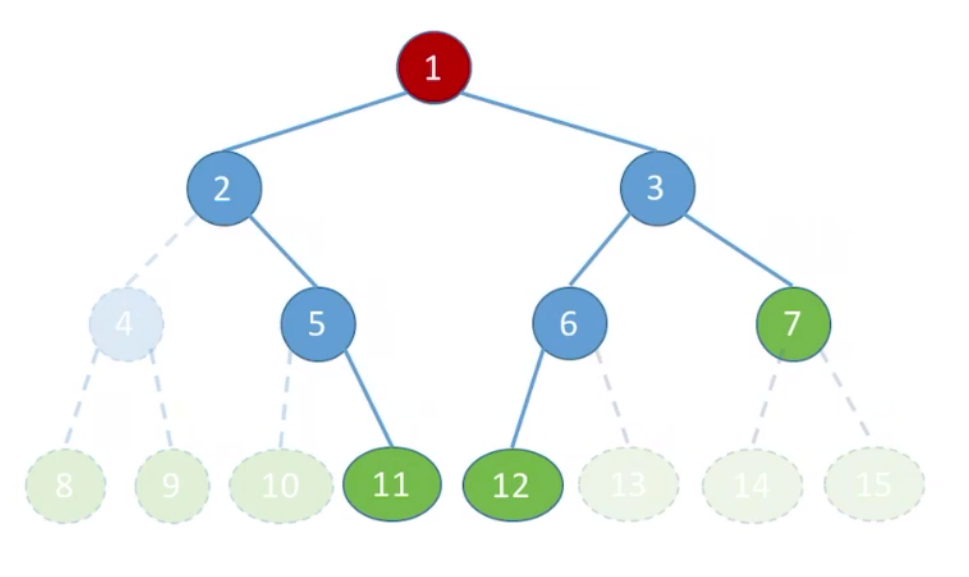
其存储结构如下:

此时可以通过结点间的编号确定结点之间关系:
但是判断结点方法不能像完全二叉树那样,只能通过创建的isEmpy字段判断。如:判断isEmpy=true所以
缺点:
这样存储会导致顺序表有大量闲置空间,最坏情况是:高度为
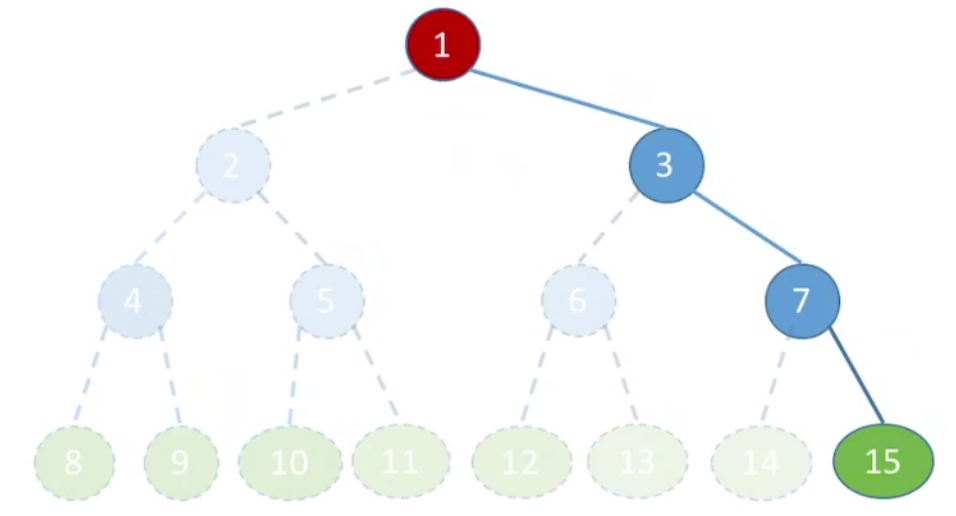
结论:二叉树的顺序存储结构,只适合存储完全二叉树。
3.3 二叉树的链式存储
存储以下二叉树结构:
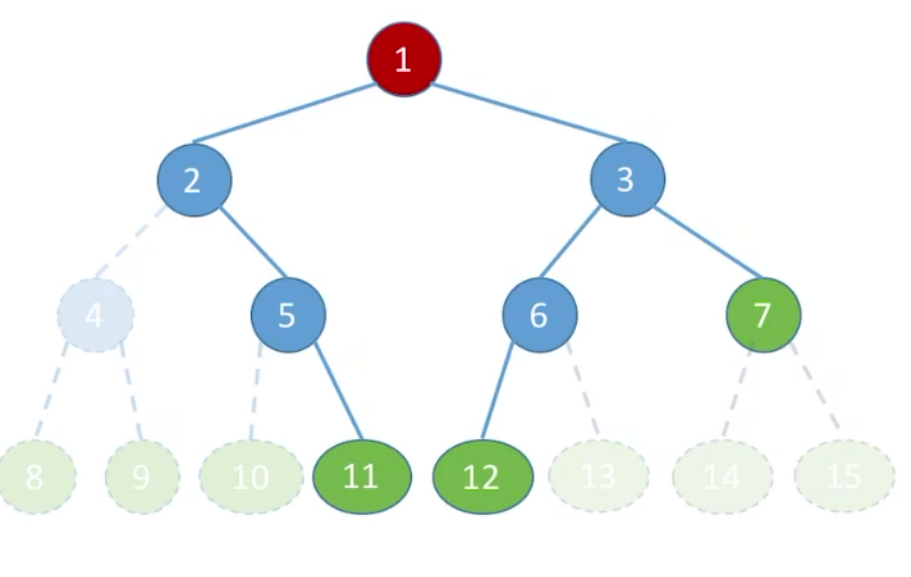
xxxxxxxxxx51//二叉树的结点(链式存储)2typedef struct BiTNode{3 ElemType data; //数据域4 struct BiTNode *lchild,*rchild; //左、右孩子指针 5}BiTNode, *BiTree;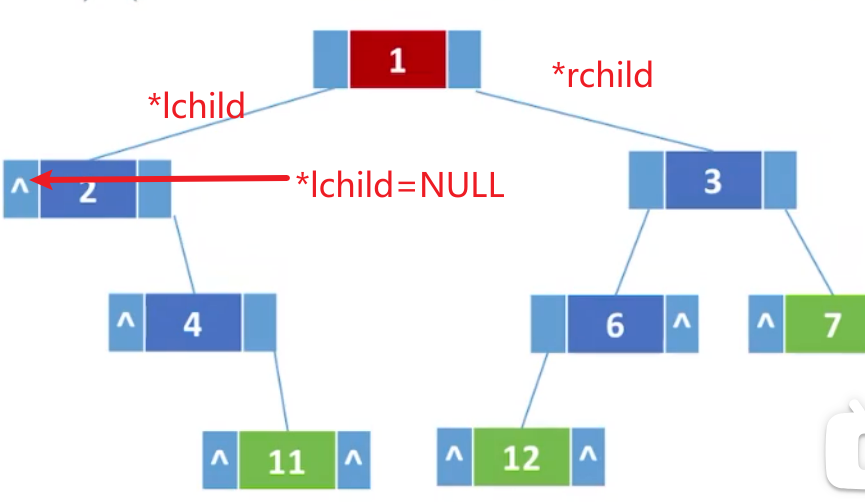
^代表这个结点指针域为空。由于每个结点都有两个指针域,如果一个二叉树有
个结点,那么它总共就有 个指针域。除了根结点,每个结点头上都至少有一个指针连接,即有 个指针,故空指针个数为: 个
完整定义代码:
xxxxxxxxxx221struct ElemType{2 int value;3};4typedef struct BiTNode{5 ElemType data;6 struct BiTNode *child,*rchild;7}BiTNode, *BiTree; 8
9//定义一棵空树10BiTree root = NULL; 11//插入根节点12root=(BiTree)malloc(sizeof(BiTNode));13root->data = {1};14root->lchild = NULL;15root->rchild = NULL;16
17//插入新结点18BiTNode *p=(BiTNode*)malloc(sizeof(BiTNode));19p->data = {2};20p->lchild = NULL;21p->rchild = NULL;22root->lchild=p;//作为根节点的左孩子找到指定结点左
找到
xxxxxxxxxx61typedef struct BiTNode{2 ElemType data;3 //数据域4 struct BiTNode *lchild,*rchild; //左、右孩子指针5 struct BiTNode *parent; //父结点指针6}BiTNode,*BiTree;3.4 二叉树遍历
二叉树递归特性:二叉树要么是个空二叉树,要么就是由"根节点
三种遍历方法
按照这种特性可以制定三种常考的遍历规则:
先序遍历:根左右(
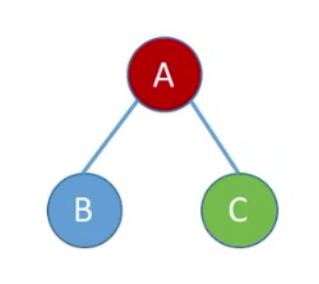
上图二叉树三种遍历方式为:
先序遍历:
较为复杂二叉树如下:
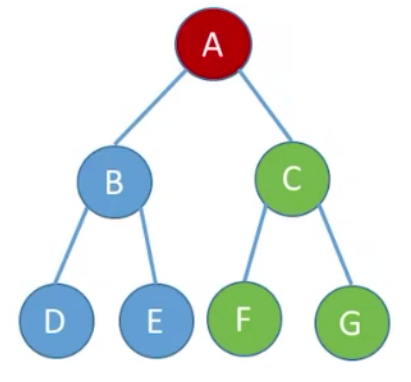
遍历方式如如下:
先序遍历:
算法表达式分析数:对于表达式:
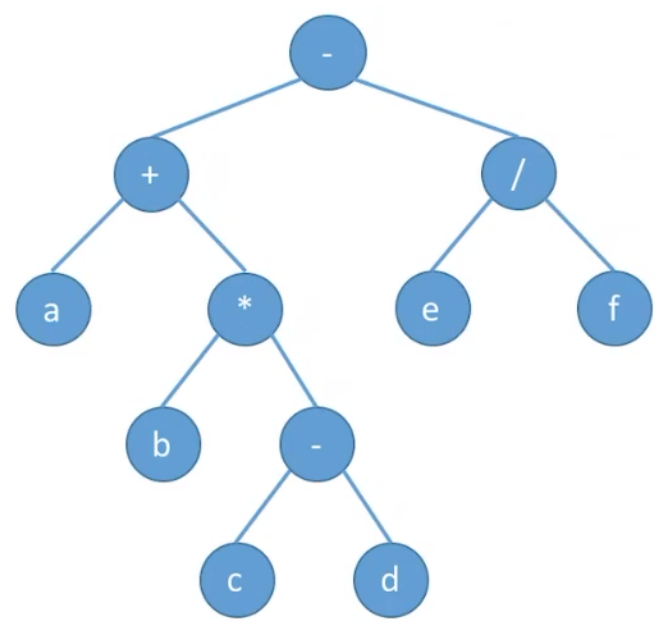
先序遍历:
中序遍历:
后序遍历:
由此可知:先序遍历
三种遍历实现方式如下:
xxxxxxxxxx241//先序遍历2void Pre0rder(BiTree T){3 if (T!=NULL){4 visit(T); //访问根结点5 Pre0rder(T->lchild); //递归遍历左子树6 Pre0rder(T->rchild); //递归遍历右子树7 }8}9//中序遍历10void Pre0rder(BiTree T){11 if (T!=NULL){12 Pre0rder(T->lchild); //递归遍历左子树13 visit(T); //访问根结点14 Pre0rder(T->rchild); //递归遍历右子树15 }16}17//后序遍历18void Pre0rder(BiTree T){19 if (T!=NULL){20 Pre0rder(T->lchild); //递归遍历左子树21 Pre0rder(T->rchild); //递归遍历右子树22 visit(T); //访问根结点23 }24}先序遍历(PreOrder)的操作过程如下:
若二叉树为空,则什么也不做
若二叉树非空: ①访问根结点
②先序遍历左子树
③先序遍历右子树
从根节点出发,画一条路:如果左边还有没走的路,优先往左边走,走到路的尽头(空结点)就往回走。如果左边没路了,就往右边走。如果左、右都没路了,则往上面走。先序遍历
是在第一次路过时访问结点。
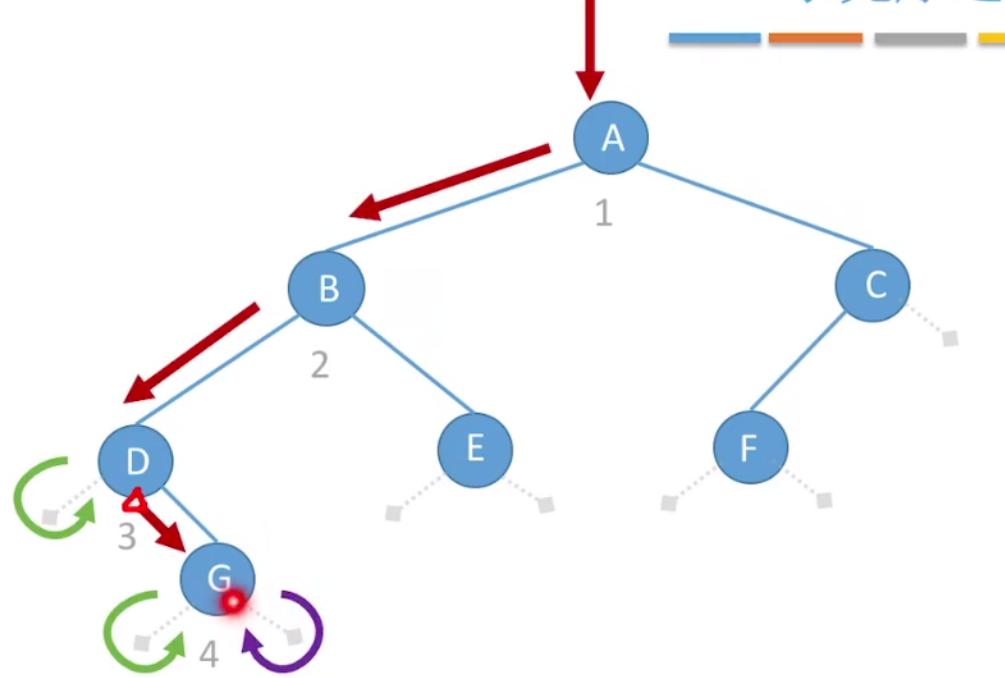
中序遍历和后续遍历同上,差别在于访问结点顺序不一样。
应用:求下面树的深度
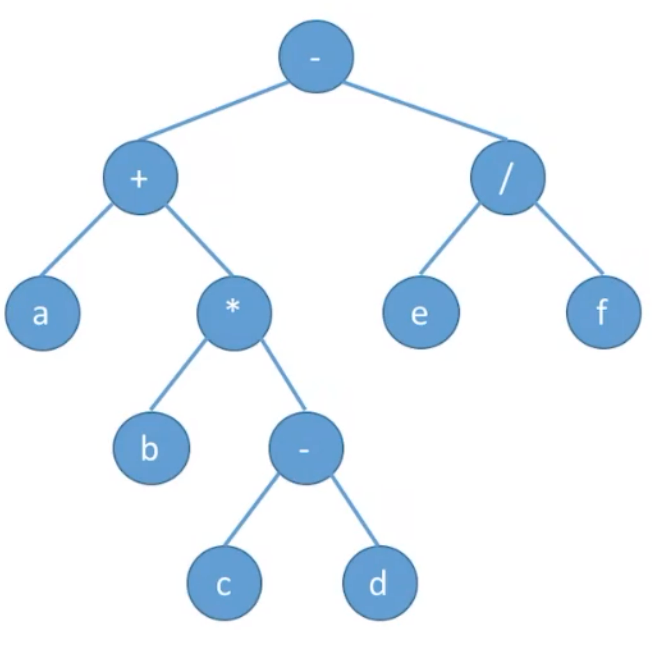
xxxxxxxxxx101int treeDepth(BiTree T){2 if (T == NULL) {3 return 0;4 }else {5 int l = treeDepth(T->lchild);6 int r = treeDepth(T->rchild);7 //树的深度=Max (左子树深度/右子树深度+1)8 return (l>r)?l+1:r+1;9 }10}上面算法通过递归特性,通过退栈,每退一次右子树的右结点,则
r+1。遇到NULL结点时,进行退栈。
二叉树层序遍历
层序遍历是每次都要判断一个结点
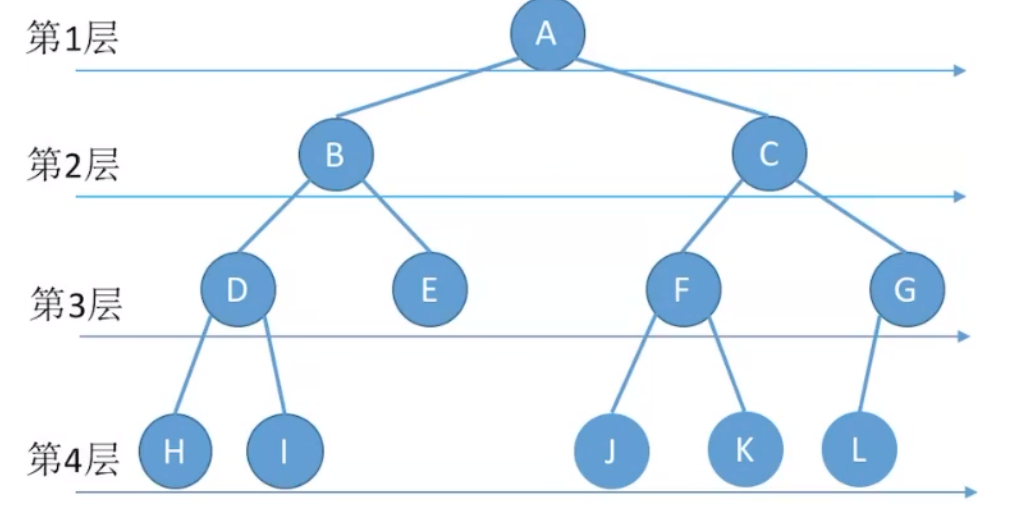
算法思想: ①初始化一个辅助队列 ②根结点入队 ③若队列非空,则队头结点出队,仿问该结点,并将其左、右孩子插入队尾(如果有的话) ④重复,知道队列为空
代码实现:
xxxxxxxxxx141void LevelOrder(BiTree T){2 LinkQueue Q;3 InitQueue(Q); //初始化辅助队列4 BiTree p;5 EnQueue(Q,T); //将根结点入队.6 while(!IsEmpty(Q)){ //队列不空则循环7 DeQueue(Q,p); //队头结点出队8 visit(p); //访问出队结点9 if(p->lchild!=NULL)10 EnQueue(Q,p->lchild); //左孩子入队11 if(p->rchild!=NULL)12 EnQueue(Q,p->rchild);//右孩子入队13 }14}结构定义:
xxxxxxxxxx131//二叉树的结点(链式存储)2typedef struct BiTNode{3 char data;4 struct BiTNode *lchild,*rchild;5}BiTNode,*BiTree;6//链式队列结点7typedef struct LinkNode{8 BiTNode * data;9 struct LinkNode *next;10}LinkNode;11typedef struct{12 LinkNode *front,*rear; //队头队尾D13}LinkQueue;结构定义第
行,我们并不需要保存整个树结点,只需要保存这个树结点的指针即可。
3.5 通过遍历序列构造二叉树
给定以下中序遍历序列:
其二叉树树结构可能为以下几种情况:
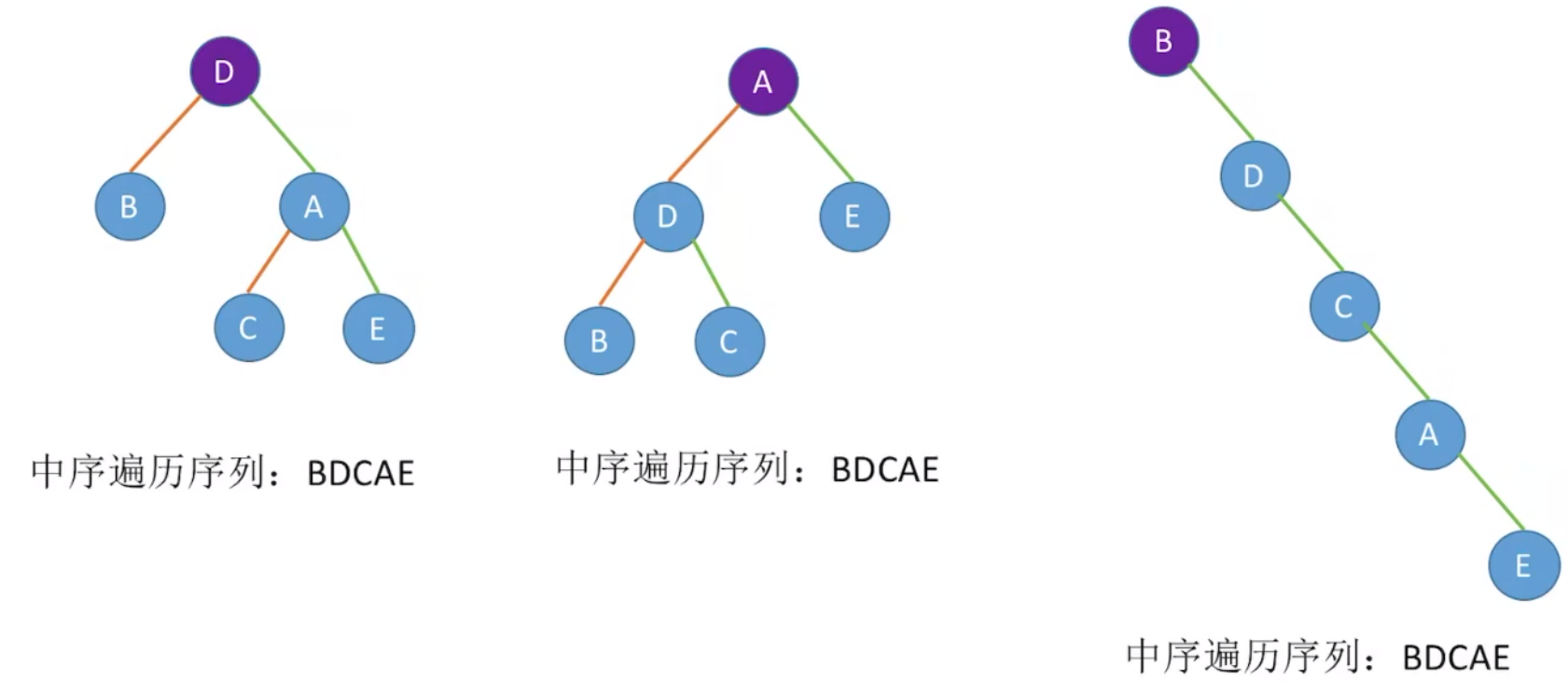
同样可以得到一个结论:若只给出二叉树的前
但如果给出中序
遍历序列特点:
- 前序遍历序列左边元素是根结点
- 后续序列的右边元素是根结点
- 中序序列可以通过前
- 层序遍历序列从左往右都是根结点。

先由前序遍历序列得出根结点
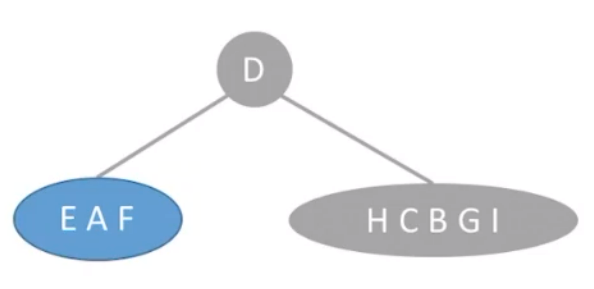
左子树元素为:
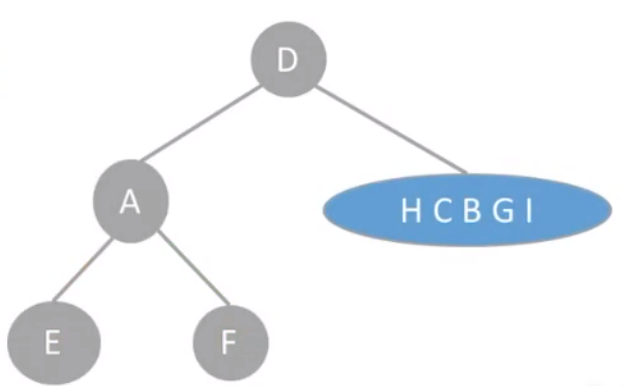
右子树
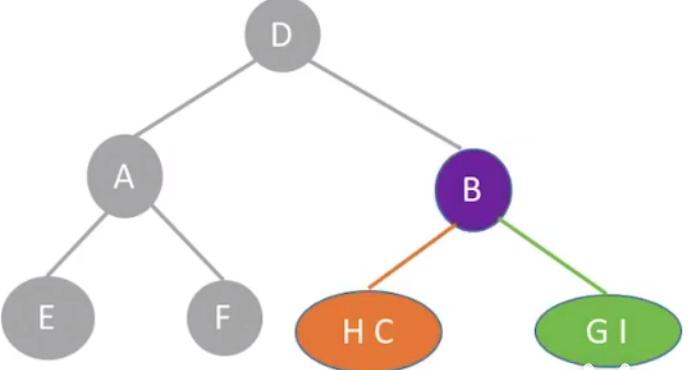
再根据前序遍历序列得出左子树
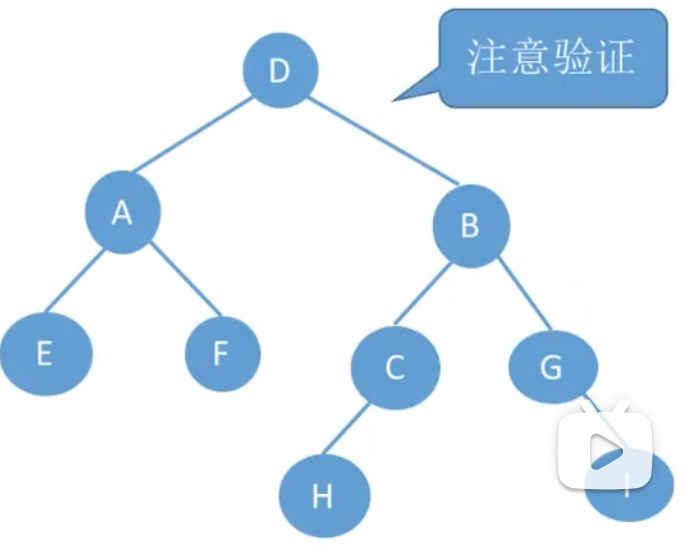

注意:必须要知道中序遍历序列才能推出二叉树结构。
3.6 线索二叉树
线索二叉树概念
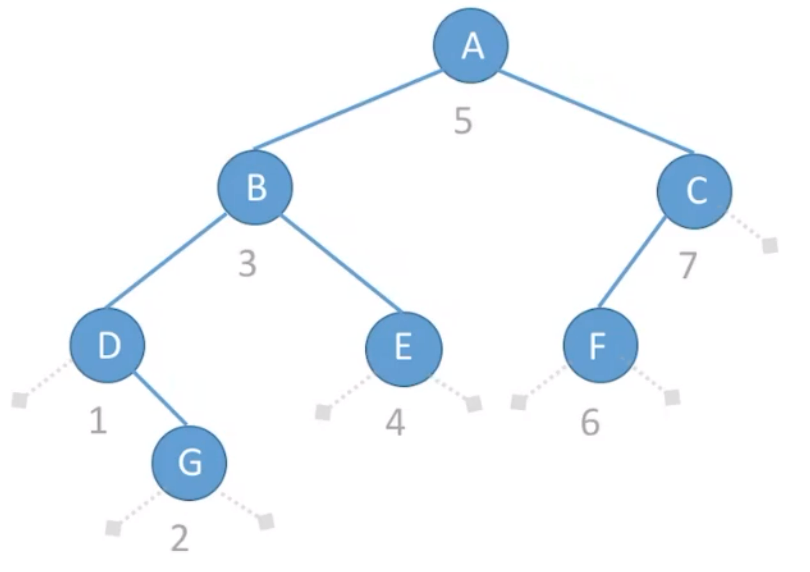
如上图二叉树结构,假设此时从
再看
从根节点出发,重新进行一次中序遍历,指针
②同样找后继方法相同。当
这样缺点是:每次必须从根结点开始,找前驱、后继很不方便。
此时就需要线索二叉树解决这个问题。
一个有
个结点的二叉树,有 个空链域。这些空链域可用来记录前驱、后继的信息。
上面的二叉树结构我们可以将其线索化,将结点空链域指向其前驱或后继(左指针指向前驱,右指针指向后继)。
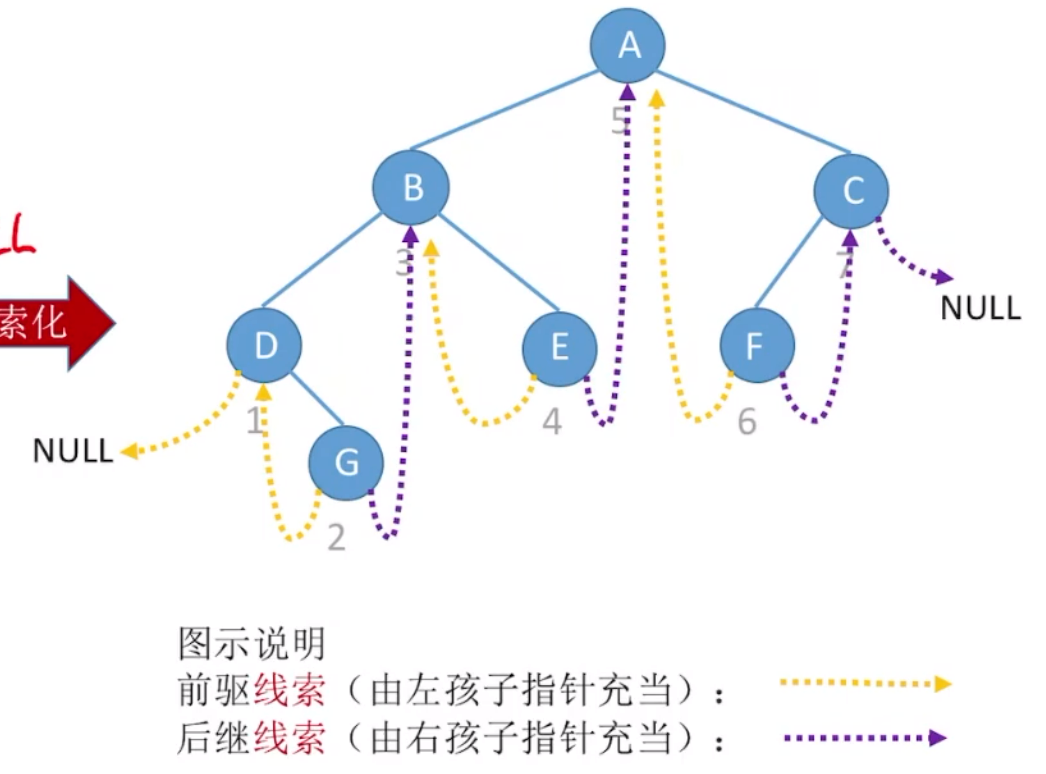
指向前驱后继的指针称为"线索"。代码实现:
xxxxxxxxxx71//线索二叉树结点2typedef struct ThreadNode{3 ElemType data;4 struct ThreadNode *lchild,*rchild;5 int ltag, rtag;6 //左、右线索标志7}ThreadNode, *ThreadTree;
,表示指针指向孩子
,表示指针是"线索"
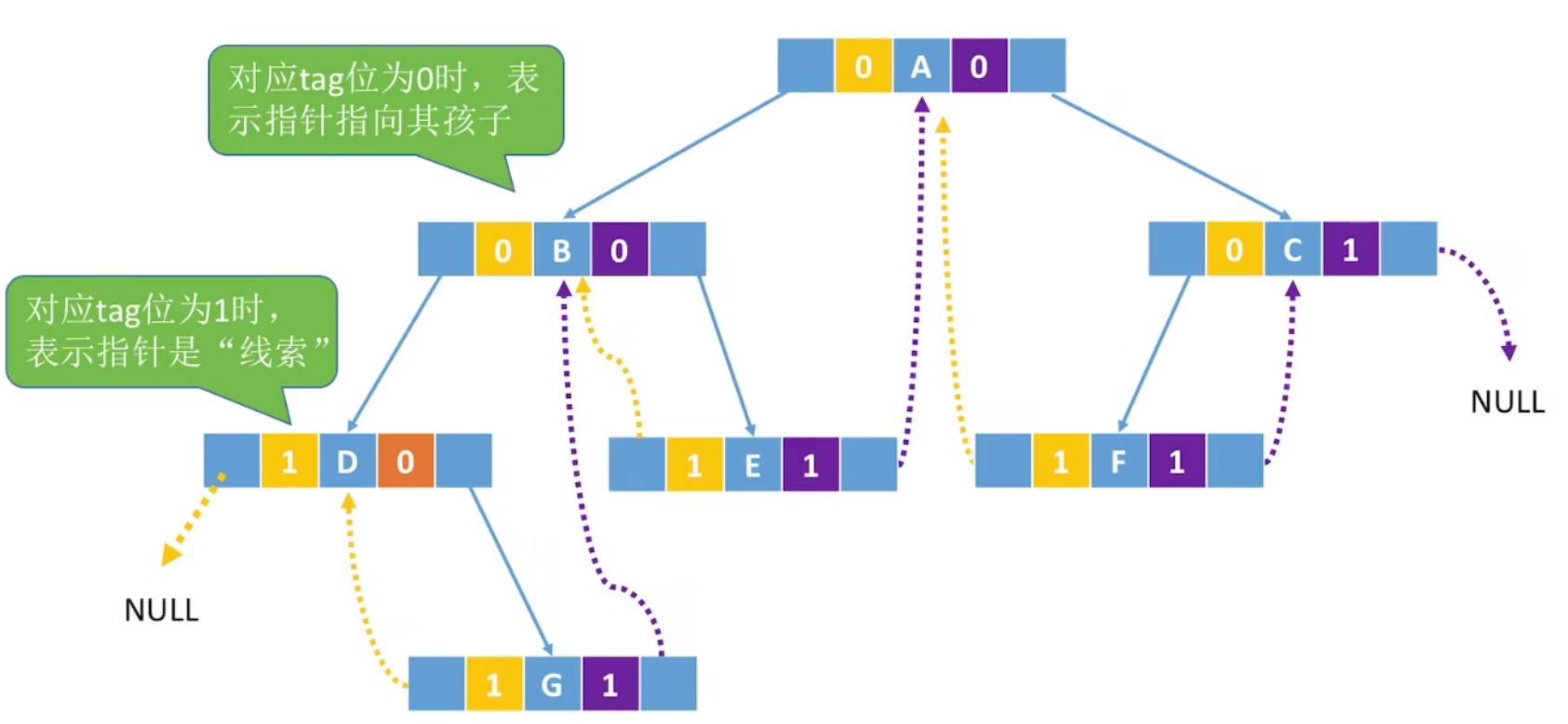
先序、后序原理同中序。

线索二叉树代码实现
方法一:以中序遍历为例用
xxxxxxxxxx191//中序遍历2void InOrder(BiTree T){3 if(T!=NULL){4 InOrder(T->lchild); //递归遍历左子树 5 visit(T) //访问根结点6 InOrder(T->rchild); //递归遍历右子树7 }8}9//访问结点q10void visit(BiTNode *q){11 if (q==p) //当前访问结点刚好是结点p12 final = pre; //找到p的前驱13 else 14 pre = q; //pre指向当前访问的结点15}16//辅助全局变量,用于查找结点p的前驱17BiTNode *p; // p指向目标结点18BiTNode * pre=NULL; //指向当前访问结点的前驱一19BiTNode * final=NULL; //用于记录最终结果方法二:同样以中序遍历为例,一边遍历一边线索化
xxxxxxxxxx441ThreadNode *pre=NULL;2
3//线索二叉树结点4typedef struct ThreadNode{5 ElemType data;6 struct ThreadNode *lchild,*rchild;7 int ltag, rtag;8 //左、右线索标志9}ThreadNode, *ThreadTree;10
11//中序遍历二叉树,一边遍历一边线索化12void InThread (ThreadTree T) {13 if(T!=NULL) {14 InThread(T->lchild);15 //中序遍历左子树16 visit(T);17 //访问根节点18 InThread(T->rchild) ;19 //中序遍历右子树20 }21}22
23//访问结点24void visit (ThreadNode *q) {25 if(q->lchild==NULL){//左子树为空,建立前驱线索26 q->lchild=pre;27 q->ltag=1;28 }29 if(pre!=NULL&&pre->rchild==NULL){30 pre->rchild=q; //建立前驱结点的后继线索31 pre->rtag=1;32 }33 pre=q; 34}35
36void CreateInThread (ThreadTree T){37 pre=NULL; //pre初始为NULL38 if(T!=NULL){ //非空二叉树才能线索化39 InThread(T);//中序线紧化二叉树40 if (pre->rchild==NULL)41 pre->rtag=1; //处理遍历的最后一个结点42
43 }44}上面代码第
行最后还要检查 的 是否为 ,如果是,则令
要特别注意先序线索化,由于先序线索化要先访问根结点:
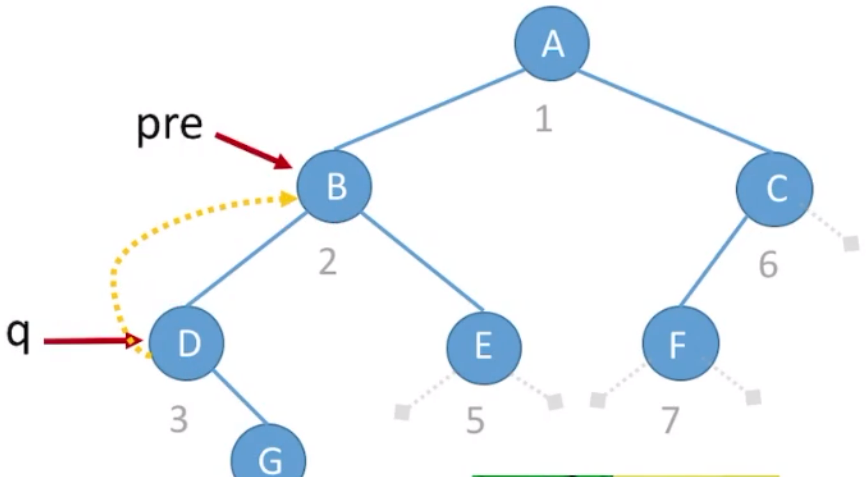
当上面代码执行到q->lchild=pre;,在执行InThread(T->lchild);时,q指针会回到InThread(T->lchild);时先判断tag变量的值,看是否为真结点。修改代码如下:
xxxxxxxxxx91//先序遍历二叉树,一边遍历一边线索化2void PreThread(ThreadTree T) {3 if(T!=NULL){4 visit(T);//先处理根节点5 if (T->ltag==0) //判断当前结点是否为真结点,而不是线索6 PreThread(T->lchild);7 PreThread(T->rchild);8 }9}后序遍历线索化同中序遍历线索化。
线索二叉树找前驱与后继
中序线索二叉树找后继
在中序线索二叉树中找到指定结点
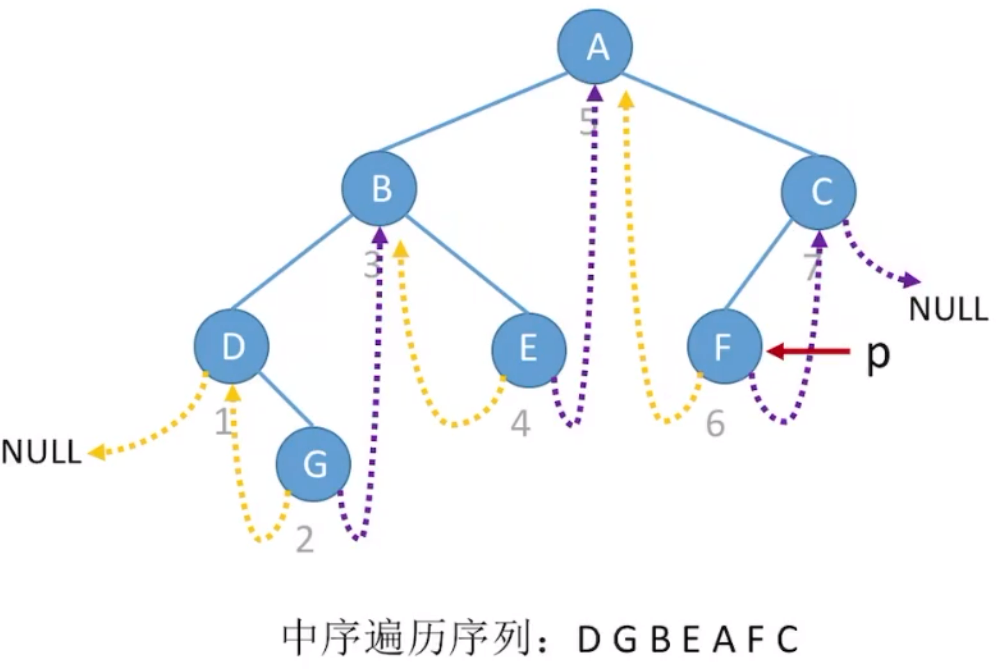
①当
p->rtag==1,则next=p->rchild的结点即为后继结点。②当
p->rtag==0时,证明结点的右子树非空,由于中序遍历顺序是左 根 右,故根结点下一个被访问的结点一定为后继。即代码实现:
xxxxxxxxxx211//找到以P为根的子树中,第一个被中序遍历的结点2ThreadNode *Firstnode (ThreadNode *p){3//循环找到最左下结点(不一定是叶结点)4while(p->ltag==0) p=p->lchild;5return p;6}78//在中序线索二叉树中找到结点p的后继结点9ThreadNode *Nextnode(ThreadNode *p){10//右子树中最左下结点11if(p->rtag==0) return Firstnode(p->rchild);12//else return p->rchild; //rtag==1 直接返回后继线索13else return NULL;14}1516//对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)17void Inorder (ThreadNode *T){18//for(ThreadNode *p=Firstnode(T); p!=NULL; p=Nextnode(p))19for(ThreadNode *p=T; p!=NULL; p=Nextnode(p))20visit(p);21}for循环中会直接找到p结点的后继结点。中序线索二叉树找前驱
①若
p->ltag==1, 则pre=p->lchild②若p->ltag==0,证明结点的左子树非空,由于中序遍历顺序是左 根 右,故根结点前一个被访问的结点一定为前驱。即代码实现:
xxxxxxxxxx211//找到以P为根的子树中,第一个被中序遍历的结点2ThreadNode *Lastnode (ThreadNode *p){3//循环找到最左下结点(不一定是叶结点)4while(p->rtag==0) p=p->rchild;5return p;6}78//在中序线索二叉树中找到结点p的后继结点9ThreadNode *Prenode(ThreadNode *p){10//右子树中最左下结点11if(p->ltag==0) return Lastnode(p->lchild);12//else return p->rchild; //rtag==1 直接返回后继线索13else return NULL;14}1516//对中序线索二叉树进行中序遍历(利用线索实现的非递归算法)17void Inorder (ThreadNode *T){18//for(ThreadNode *p=Firstnode(T); p!=NULL; p=Nextnode(p))19for(ThreadNode *p=T; p!=NULL; p=Prenode(p))20visit(p);21}for循环中会直接找到p结点的前驱结点。先序线索二叉树找后继
①当
p->rtag==1,则next=p->rchild的结点即为后继结点。②当
p->rtag==0时,证明结点的右子树非空,由于先序遍历顺序是根 左 右,有以下几种情况:- 若
p有左孩子,则先序后继为左孩子。 - 假设
p没有左孩子,则先序后继为右孩子。
- 若
先序线索二叉树找前驱
①若
p->ltag==1, 则pre=p->lchild②若p->ltag==0,情况下先序遍历,左右子树中的结点只可能是根的后继,不可能是前驱。这种情况下只能用土办法从头开始遍历。但二叉树为三叉链表存储结构(各个结点记录父结点。)的具体查找情况如下:
- 如果能找到
p的父节点,且p是左孩子:p的前驱为父结点 - 如果能找到
p的父节点,且p是右孩子,其左兄弟为空:p的前驱为父结点。 - 如果能找到
p的父节点,且p是右孩子,其左兄弟非空:p的前驱为左兄弟子树中最后一个被遍历的结点。按照先序遍历特点,设计算法时应该,优先遍历左兄弟结点右边的路走,右边路走完,找有没有左边路,以此循环找到最后一个被先序遍历的结点即为后继。 - 如果
p是树的根结点,则p没有先序前驱。
- 如果能找到
后序线索二叉树找前驱
①若
p->ltag==1, 则pre=p->lchild②若p->ltag==0,情况下后序遍历,证明p必定有左孩子,但右孩子未知。有以下几种情况:- 假设有右孩子,按照
左 右 根遍历顺序。p前驱一定是右子树当中按照后序遍历最后一个被访问结点。即p有右孩子,则后序前驱为右孩子。 - 假设没有右孩子:此时
p的后序前驱为左孩子
- 假设有右孩子,按照
后序线索二叉树找后继
①若
p->ltag==1, 则pre=p->lchild②若p->ltag==0,情况下后序遍历,按照左 右 根特点顺序,后序遍历中,左右子树中的结点只可能是根的前驱,不可能是后继。这种情况下只能用土办法从头开始遍历。但二叉树为三叉链表存储结构(各个结点记录父结点。)的具体查找情况如下:
- 如果能找到
p的父节点,且p是右孩子:p的父结点为其后继 - 如果能找到
p的父节点,且p是左孩子:p的父结点为其后继 - 如果能找到
p的父节点,且p是左孩子,其右兄弟非空:p的后继为右兄弟子树中第一个被后序遍历的结点。按照后序遍历特点,设计算法时应该,优先遍历右兄弟结点左边的路走,左边路走完,找有没有右边路,以此循环找到最后一个被后序遍历的结点即为后继。 - 如果
p是根节点,则p没有后序后继
- 如果能找到
总结:
| 中序线索二叉树 | 先序线索二叉树 | 后序线索二叉树 | |
|---|---|---|---|
| 找前驱 | √ | × | √ |
| 找后继 | √ | √ | × |
线索二叉树考点在于:怎么手算二叉树线索化、找线索二叉树前驱和后继。
4. 树的存储与遍历
树是一种递归定义的数据结构。
树是
- 有且仅有一个特定的称为根的结点。
- 当
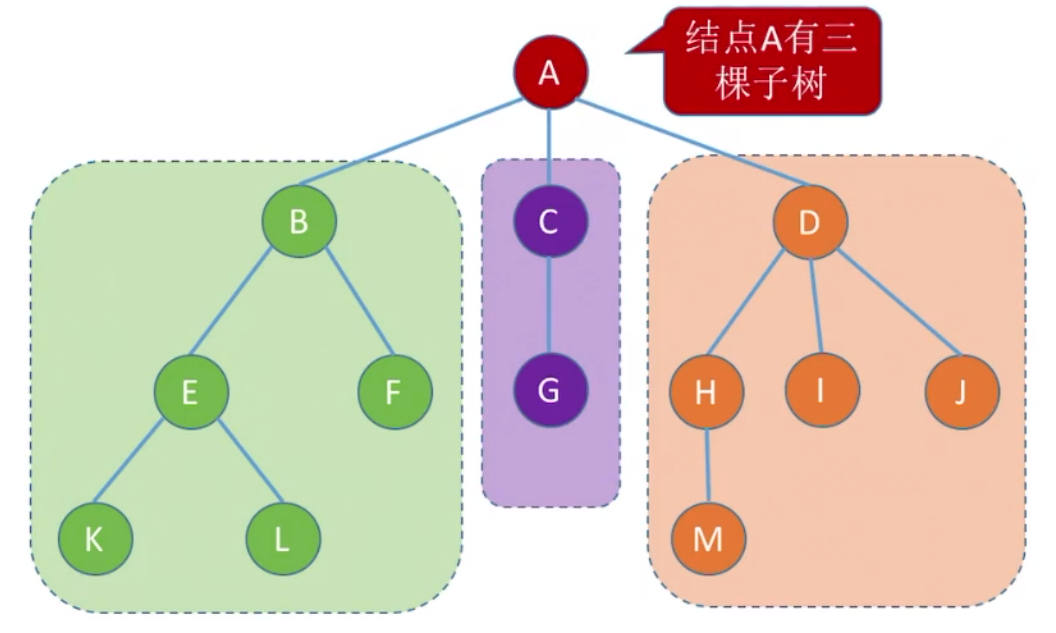
4.1 树与森林的存储方法
双亲表示法
双亲表示法:每个结点中保存指向双亲的"指针"。
树特点是树种任意一个结点都有且仅有一个双亲,所以在每个结点种保存指向"双亲"的指针。如要保存下面树结构:

结构体如下:
xxxxxxxxxx121//树中最多结点数3typedef struct{4 ElemType data; //树的结点定义5 //数据元素6 int parent; //双亲位置域7}PTNode;8//树的类型定义9typedef struct{ 10 PTNode nodes [MaxSize];//双亲表示11 int n;//结点数12}PTree;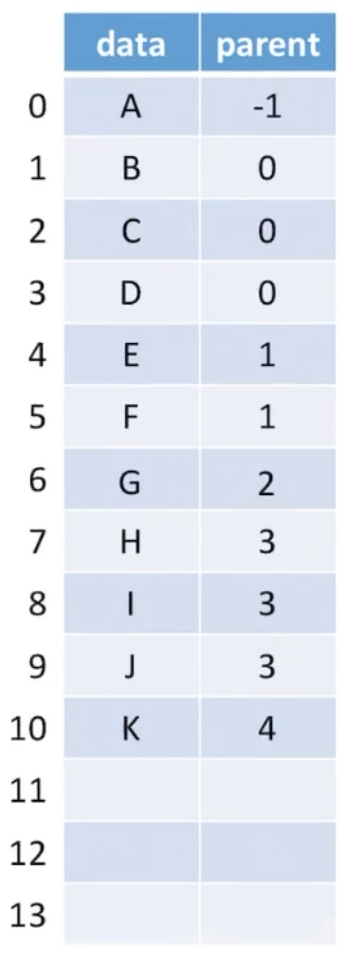
如果新增加元素,无需按照逻辑上的次序存储。如:在k结点添加左孩子k和右孩子l,此时k,l结点插入顺序无所谓。
删除方案有两种:
- 将被删除元素的
parent位置域指针值设置为:-1 - 删除该位置元素,并将尾部元素填充至该位置。
注意以上操作都要结点数n-1
如果删除的是根结点,那么要让根结点所有子结点同时删除,此时双亲表示法缺点就暴露出来:查指定结点的孩子只能从头遍历,对比该结点的parent值是否是删除根结点的位置。
如果被删除根结点子元素很多,那么使用第一种删除方案会导致空数据增多,增加遍历的时间复杂度。
孩子表示法
孩子表示法:顺序存储各个节点,每个结点中保存孩子链表头指针
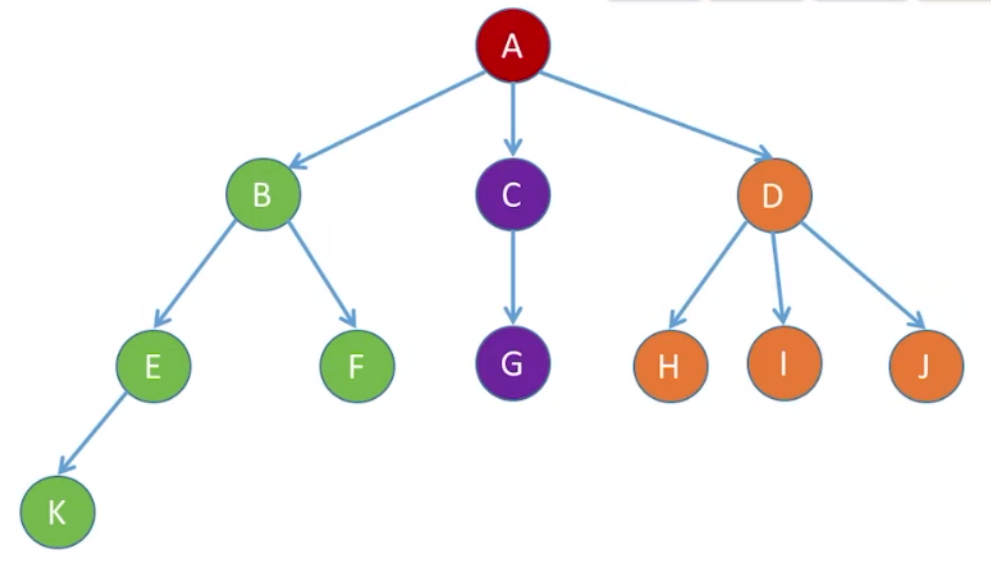
树结构结构体代码如下:
xxxxxxxxxx131struct CTNode {3 int child; //孩子结点在数组中的位置4 struct CTNode *next;//下一个孩子5};6typedef struct {7 ElemType data;8 struct CTNode *firstChild;//第一个孩子9}CTBox;10typedef struct{11 CTBox nodes[MaxSize] ;12 int n,r; //结点数和根的位置13} CTree;树结构存储结构如下:
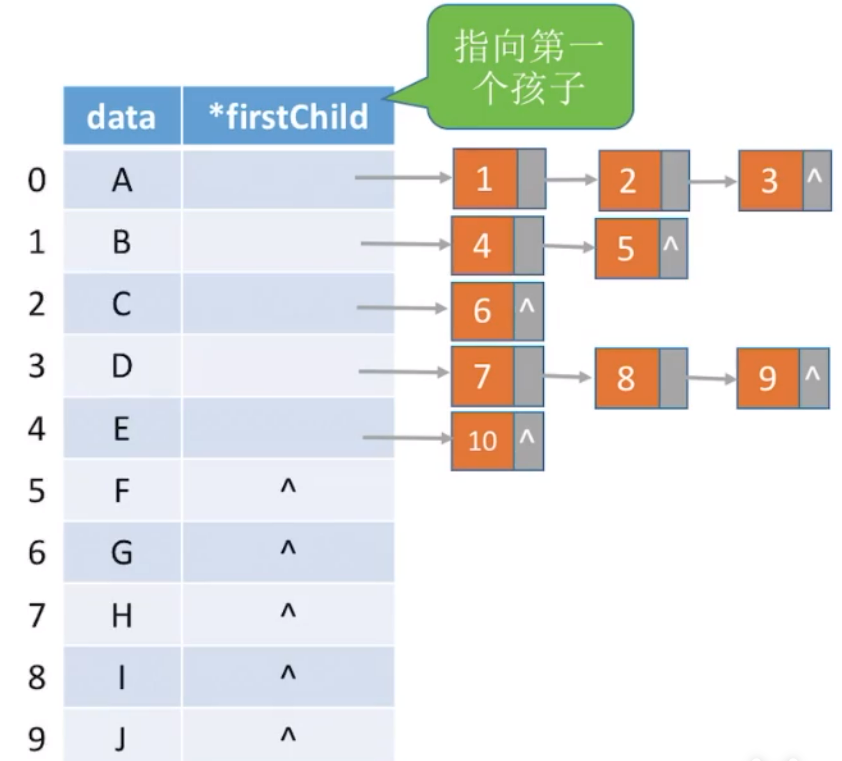
孩子兄弟表示法
孩子兄弟表示法:链式存储的方式存储一棵树。可以将树转化为二叉树的存储结构。
存储以下树结构:

树的结构存储如下:
xxxxxxxxxx41typedef struct CSNode{2 ElemType data; //数据域3 struct CSNode *firstchild,*nextsibling; //第一个孩子和右兄弟指针4}CSNode,*CSTree;*firstchild指针看作二叉树中的左指针,*nextsibling看作二叉树中的右指针。
存储过程如下:
先存储根结点
根结点左指针
*firstchild指向第一个孩子B结点,接着*nextsibling指针指向B结点的兄弟结点。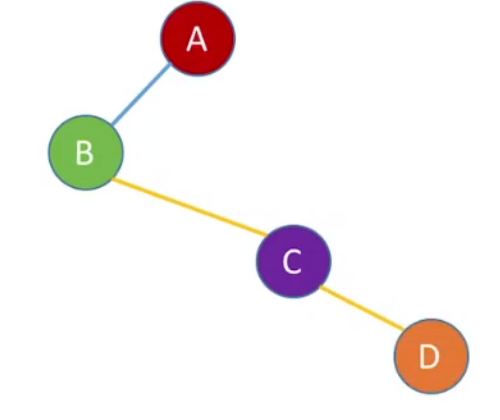
B结点的第一个孩子是E结点,*firstchild指向E;E结点兄弟是F,*nextsibling指针指向F。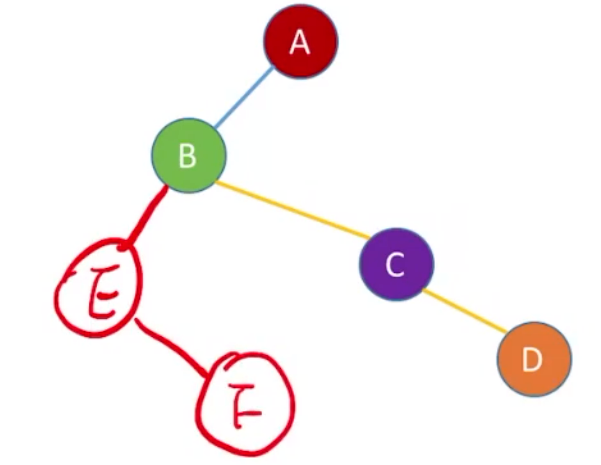
E的第一个孩子是K,*firstchild指向K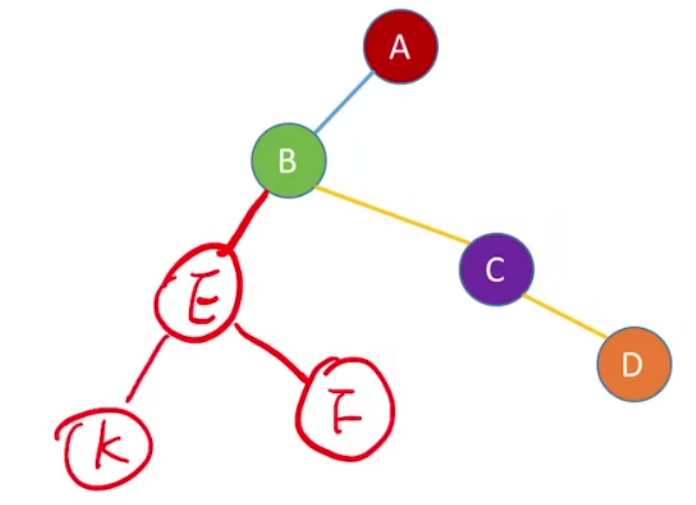
C的第一个孩子是G,*firstchild指向G;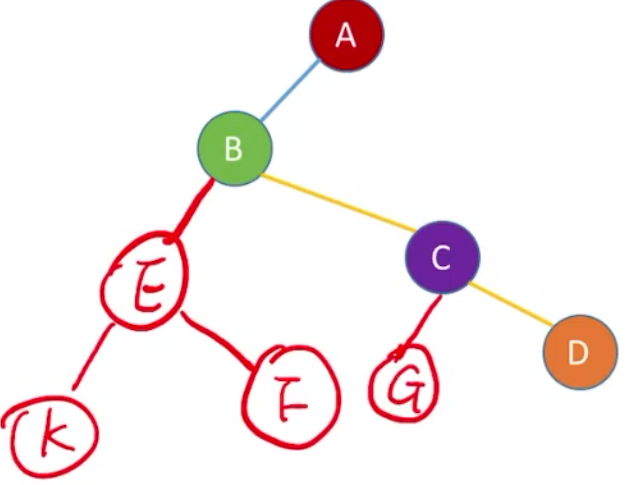
D的第一个孩子是H,*firstchild指向H;剩下的I,J都是H的兄弟结点,故H的*nextsibling指针指向I,I的*nextsibling指针指向J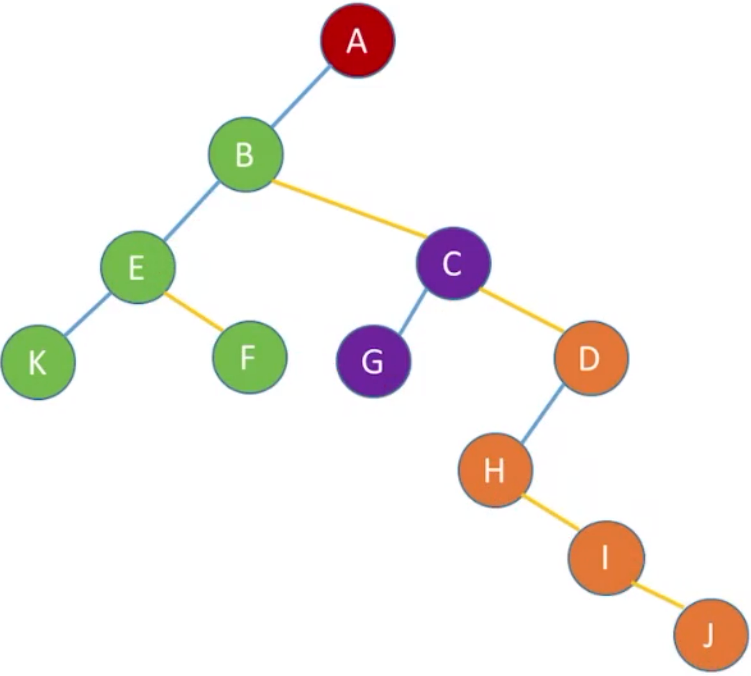
以上操作我们将树转换为了二叉树。其优点是可以用熟悉的二叉树操作来处理树。
再看一个树转换二叉树例子:
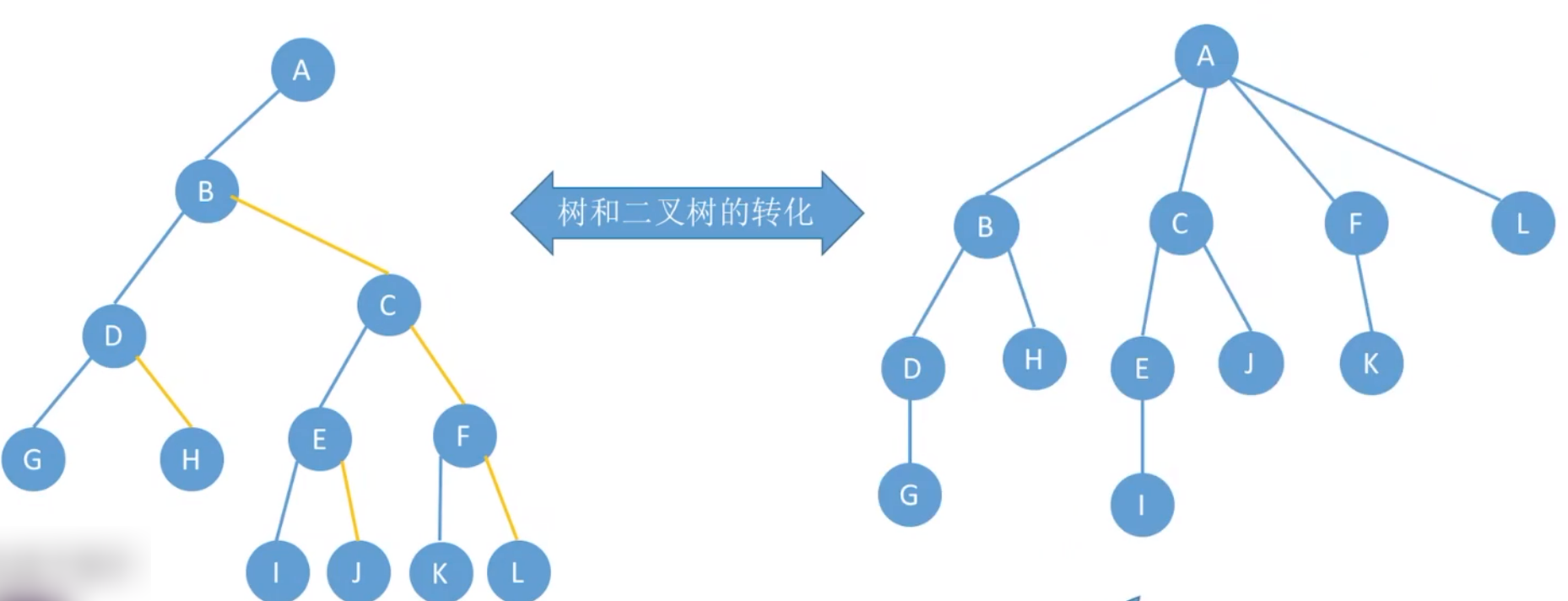
简单来说就是:树的左边都是其孩子结点,右边都是兄弟结点。
森林转换二叉树
森林。森林是
上面的孩子兄弟表示法可以将树转换成二叉树。同样的,森林也可以转换为二叉树来存储和遍历。
将以下森林转换为二叉树:

首先将这些森林的树转换为二叉树:
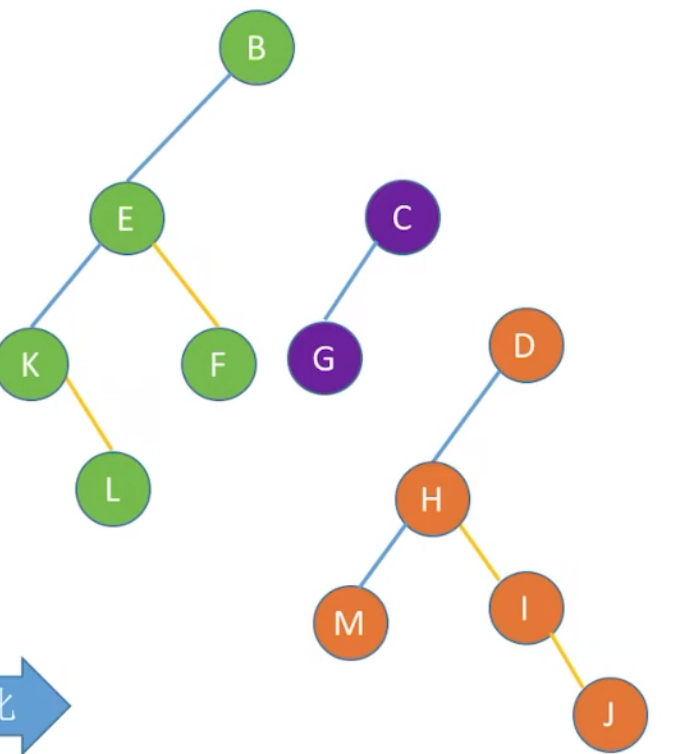
由于这些树的根结点B,C,D是平级关系,所以相连称为兄弟关系。
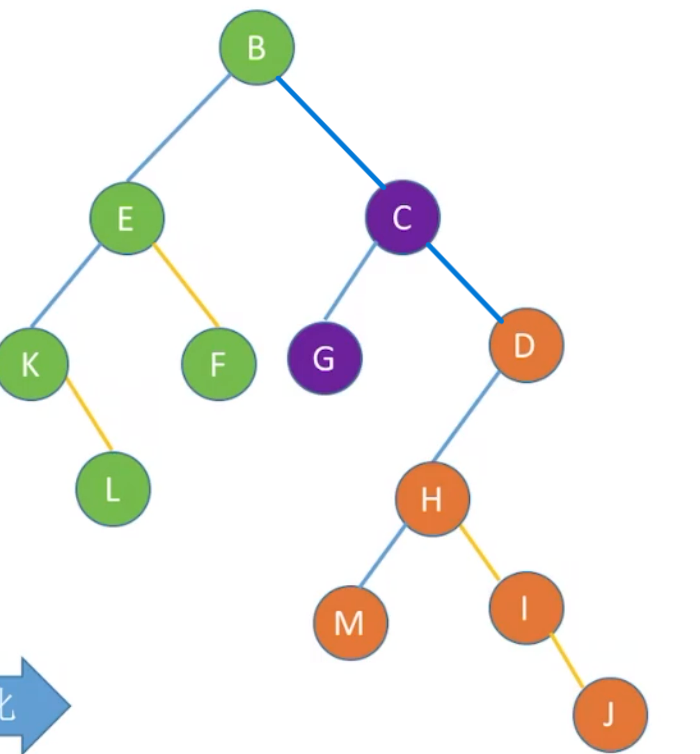
二叉树转换为森林
二叉树转换为森林是对上一节的逆用。将以下二叉树转换为森林:
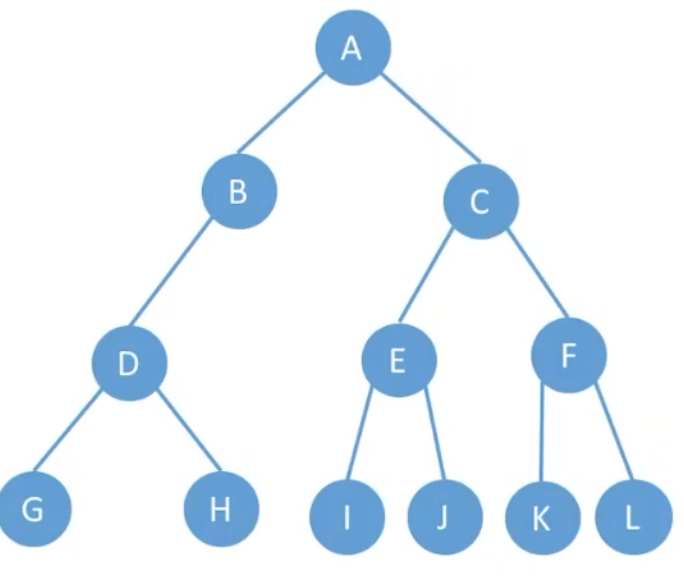
根据右边结点是兄弟结点,左边是对应兄弟结点的子结点特性:
A,C,F,L是兄弟结点,即森林树的根结点。- 剩下结点依次为上面结点子结点即可
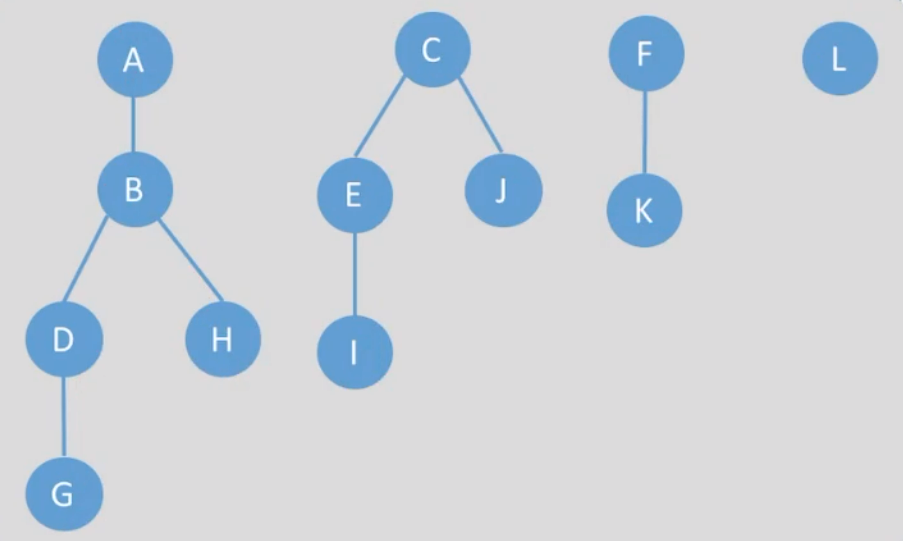
4.2 树和森林的遍历
先根遍历
先根遍历:若树非空,先访问根结点,再依次对每棵子树进行先根遍历。
伪代码实现如下:
xxxxxxxxxx81//树的先根遍历2void Pre0rder(TreeNode *R) {3 if (R!=NULL){4 visit(R) //访问根节点5 while(R还有下一个子树T)6 Pre0rder(T); //先根遍历下一棵子树 7 }8}对下面树进行遍历:
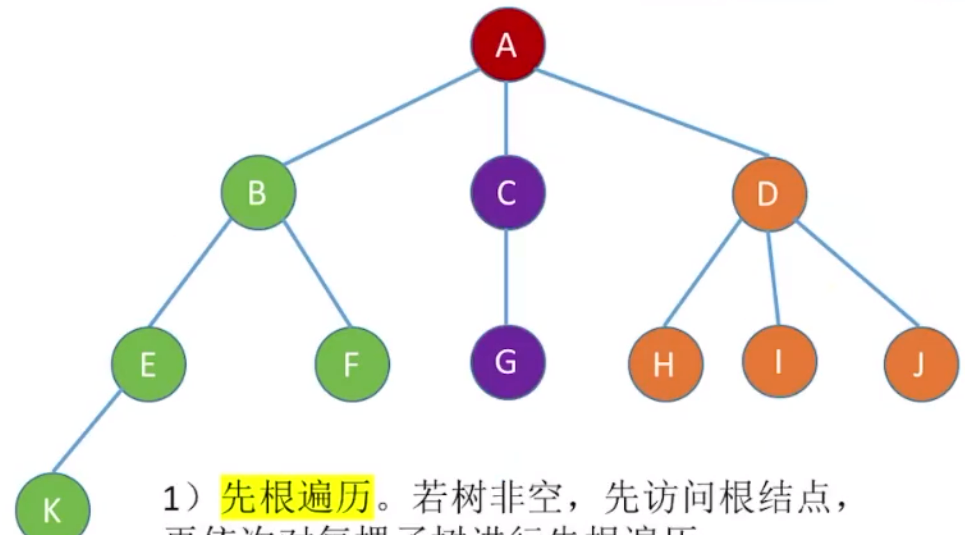
先根遍历顺序:
总结:树的先根遍历序列与这棵树相应二叉树的先序序列相同。
树的后根遍历(深度优先遍历)
后根遍历:若树非空,先依次对每棵子树进行后根遍历,最后再访问根结点。
伪代码如下:
xxxxxxxxxx81//树的后根遍历2void Pos tOrder(TreeNode *R){3 if (R!=NULL){4 while(R还有下一个子树T)5 PostOrder(T); //后根遍历下一棵子树6 visit(R); //访问根节点7 }8}对下面树进行遍历:

后根遍历顺序:
总结:树的后根遍历序列与这棵树相应二叉树的中序序列相同。
树的层次遍历(广度优先遍历)
用队列实现:
- 若树非空,则根节点入队
- 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队
- 重复
- 直到队列为空
森林的先序遍历
先序遍历森林:若森林为非空,则按如下规则进行遍历:
- 访问森林中第一棵树的根结点。
- 先序遍历第一棵树中根结点的子树森林。
- 先序遍历除去第一棵树之后剩余的树构成的森林。
遍历以下森林结构:
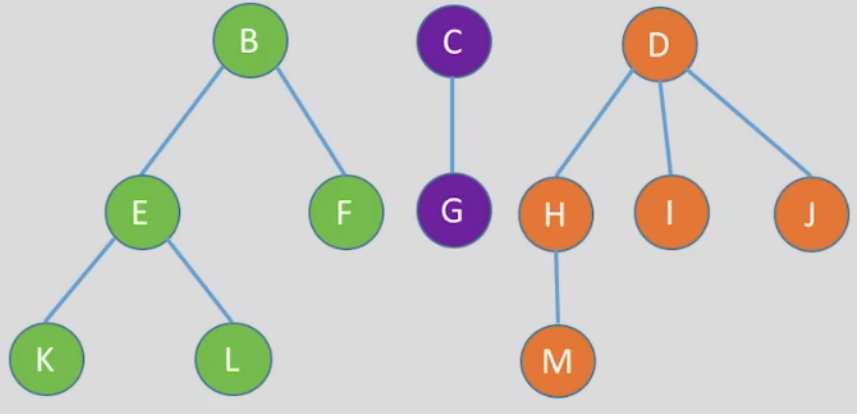
先序遍历顺序:
森林的先序遍历效果等同于依次对各个树进行先根遍历
以上算法设计时,有两层的嵌套递归,所以推荐将森林转换为二叉树,其先序遍历效果等同于依次对二叉树进行先序遍历。
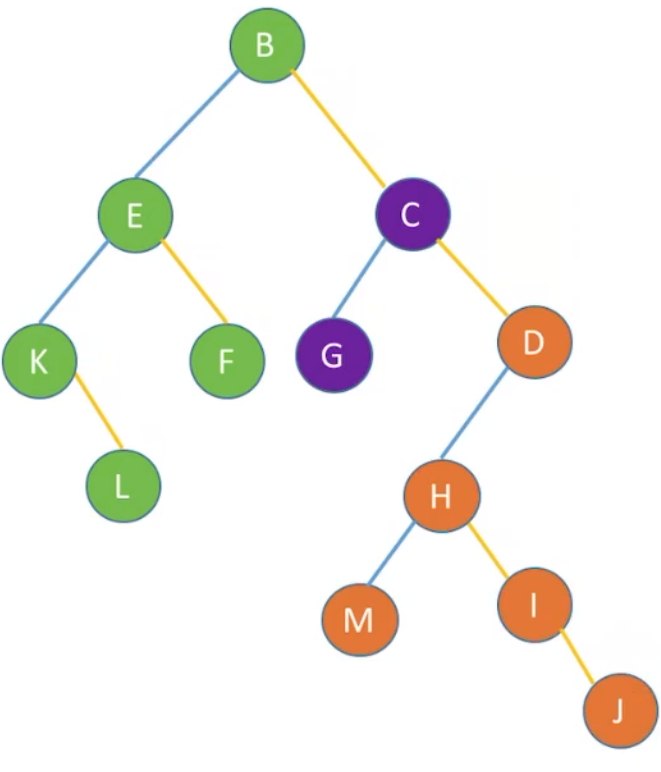
森林的中序遍历
先序遍历森林:若森林为非空,则按如下规则进行遍历:
- 中序遍历第一棵树中根结点的子树森林。
- 访问森林中第一棵树的根结点。
- 中序遍历除去第一棵树之后剩余的树构成的森林。
遍历以下森林结构:

中序遍历顺序:
森林的先序遍历效果等同于依次对各个树进行后根遍历
同样的以上算法设计时,有两层的嵌套递归,所以推荐将森林转换为二叉树,其中序遍历效果等同于依次对二叉树进行中序遍历。

总结:
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历 | 中序遍历 |
5. 哈夫曼树
结点的权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度:从树的根到该结点的路径长度( 经过的边数)与该结点上权值的乘积
树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length)
计算以下树叶子结点的带权路径长度:
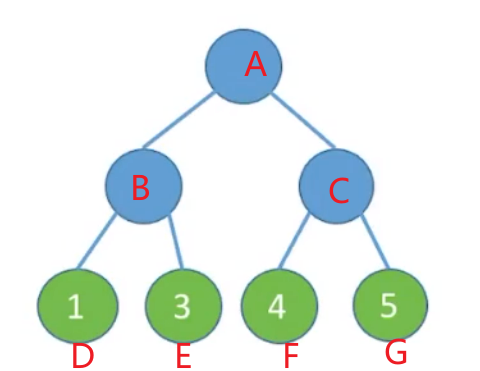
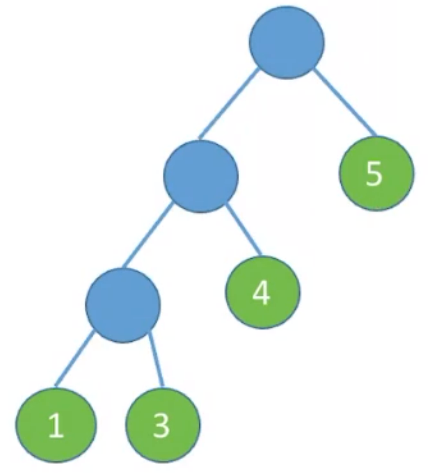
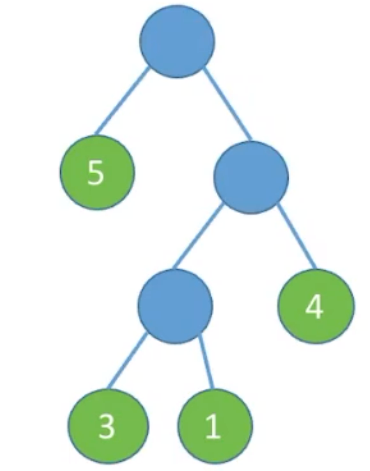
有了带权路径长度这个概念可以得到哈夫曼树定义:在含有
5.1 哈夫曼树的构造
给定
- 将这
- 构造一个新结点,从
- 从
- 重复步骤
有以下结点集合,构造哈夫曼树:
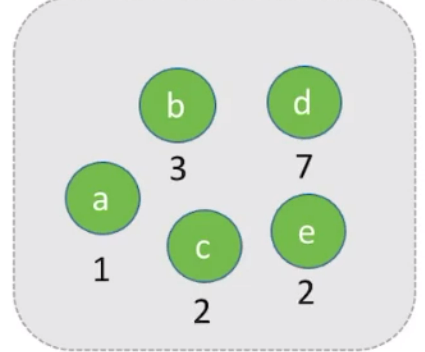
步骤:
首先将集合中最小的两个结点作为孩子结点,其根结点为两个孩子结点权值之和。
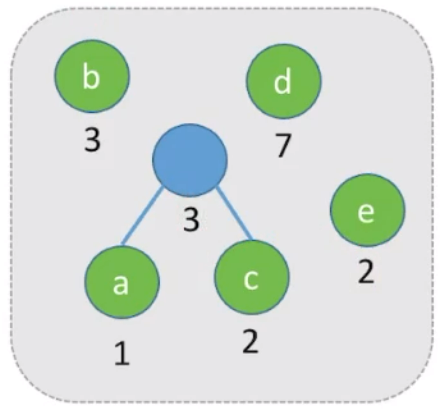
a,c结点权值较小作为孩子结点,其根结点是权值为3的结点。再将上面根结点与剩下结点集合中权值最小的结点
e做合并,根结点为3与e结点权值之和5
重复上述操作将
5和b结合,其根结点为8;8在与d结合,根结点为15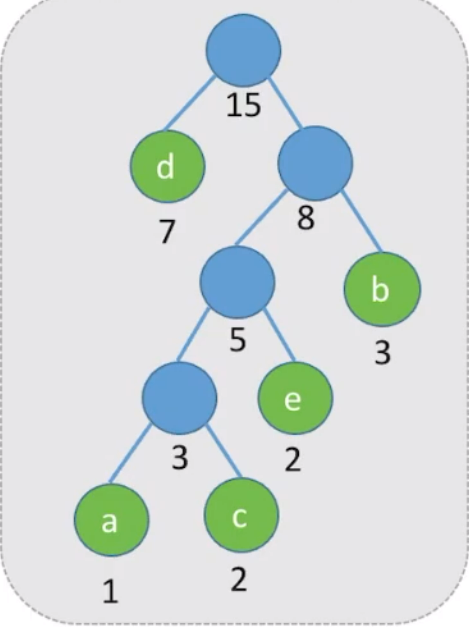
这颗树的
WPL为:这颗带权路径长度最小的二叉树就是哈夫曼树。
特点如下:
每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
哈夫曼树的结点总数为
哈夫曼树不存在度为
哈夫曼树不唯一,且
上面例子还可以构造成下面这颗哈夫曼树:
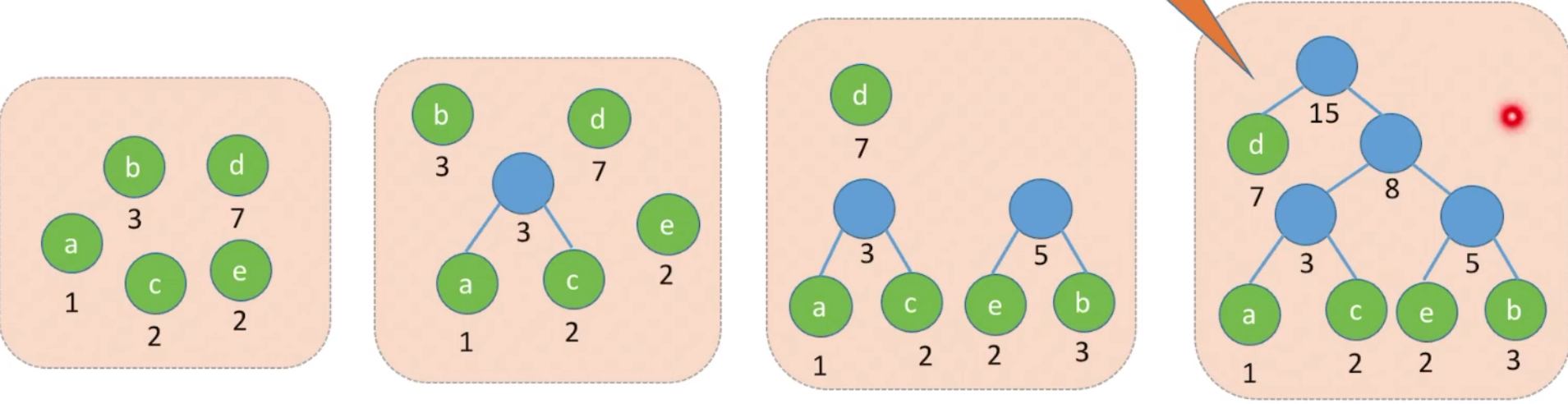
其
5.2 哈夫曼树的应用
哈夫曼树应用是:哈夫曼编码用于压缩。
哈夫曼编码:即给定一个字符集,设计一个编码方案。
分析:规定哈夫曼树左路径是
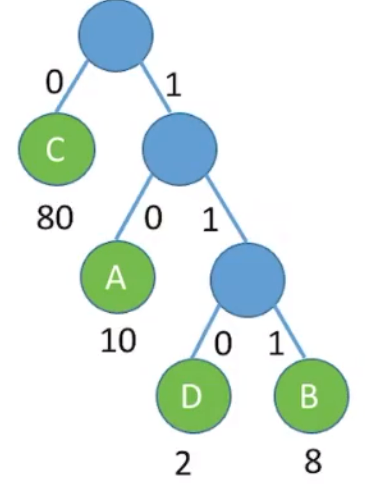
此时
则此哈夫曼树的
哈夫曼编码特点:
- 可变长度编码:允许对不同字符用不等长的二进制位表示。如上面的
- 固定长度编码:每个字符用相等长度的二进制位表示
- 若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。非前缀编码在解码的时候有歧义,如将上面
- 有哈夫曼树得到哈夫曼编码:字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树。
- 同样,哈夫曼编码不唯一。
- 上面哈夫曼编码可以用于压缩存储。
八. 并查集
注:并查集( Disjoint Set)是逻辑结构:是集合的一种具体实现,只进行"并"和"查"两种基本操作。
如果给定多个元素,将各个元素划分为若千个互不相交的子集,这些子集就叫做集合。
可以用森林结构表示各个子集。以下子集:
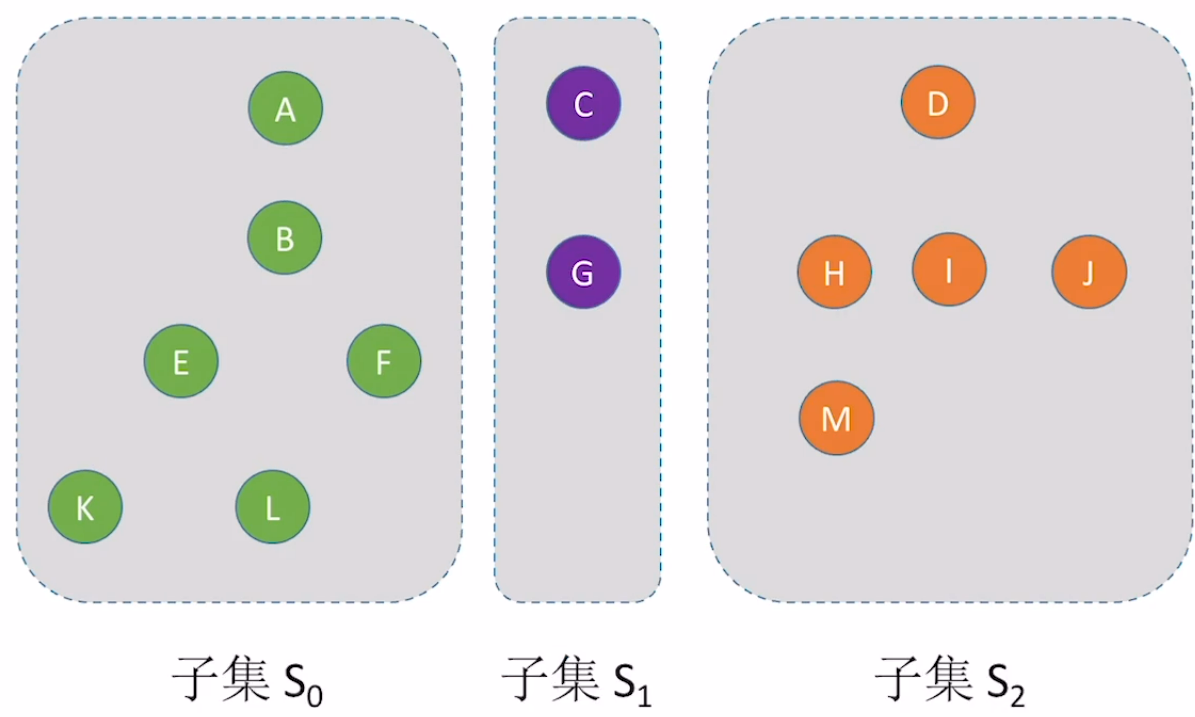
可以用森林表示结构:
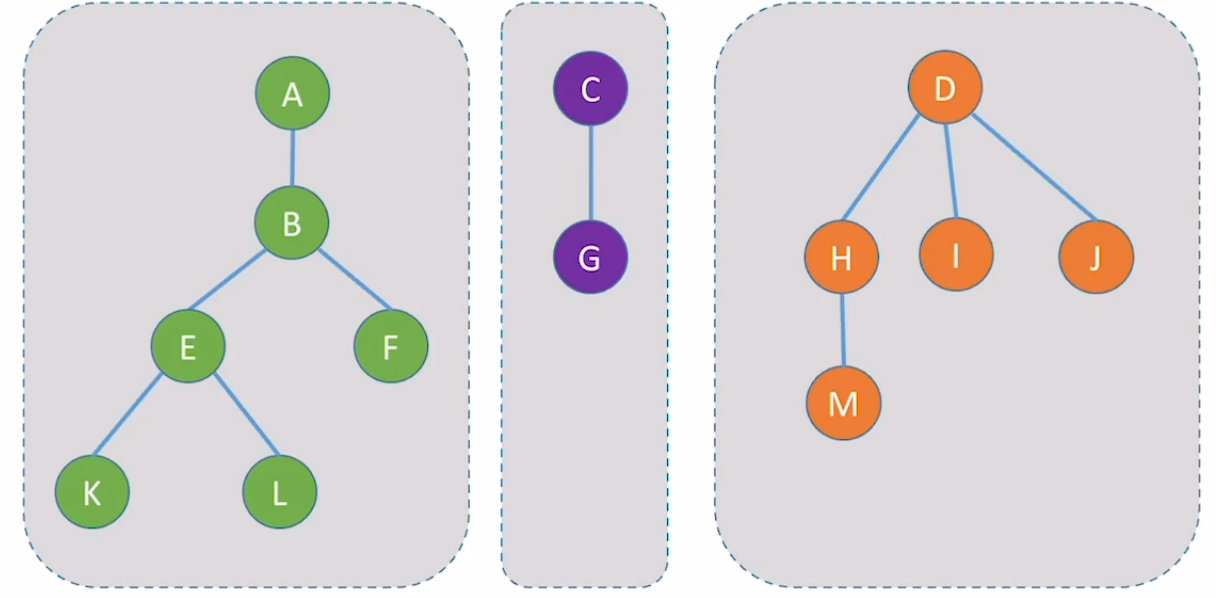
集合两个常见操作:①查:给定元素,找到该元素所属的集合(根结点);②并:将一棵树的根结点并到另一个树下。
可以看到以上两个操作需要都需要由下往上找到根结点,所以我们需要用到树的双亲表示法来存储集合结构
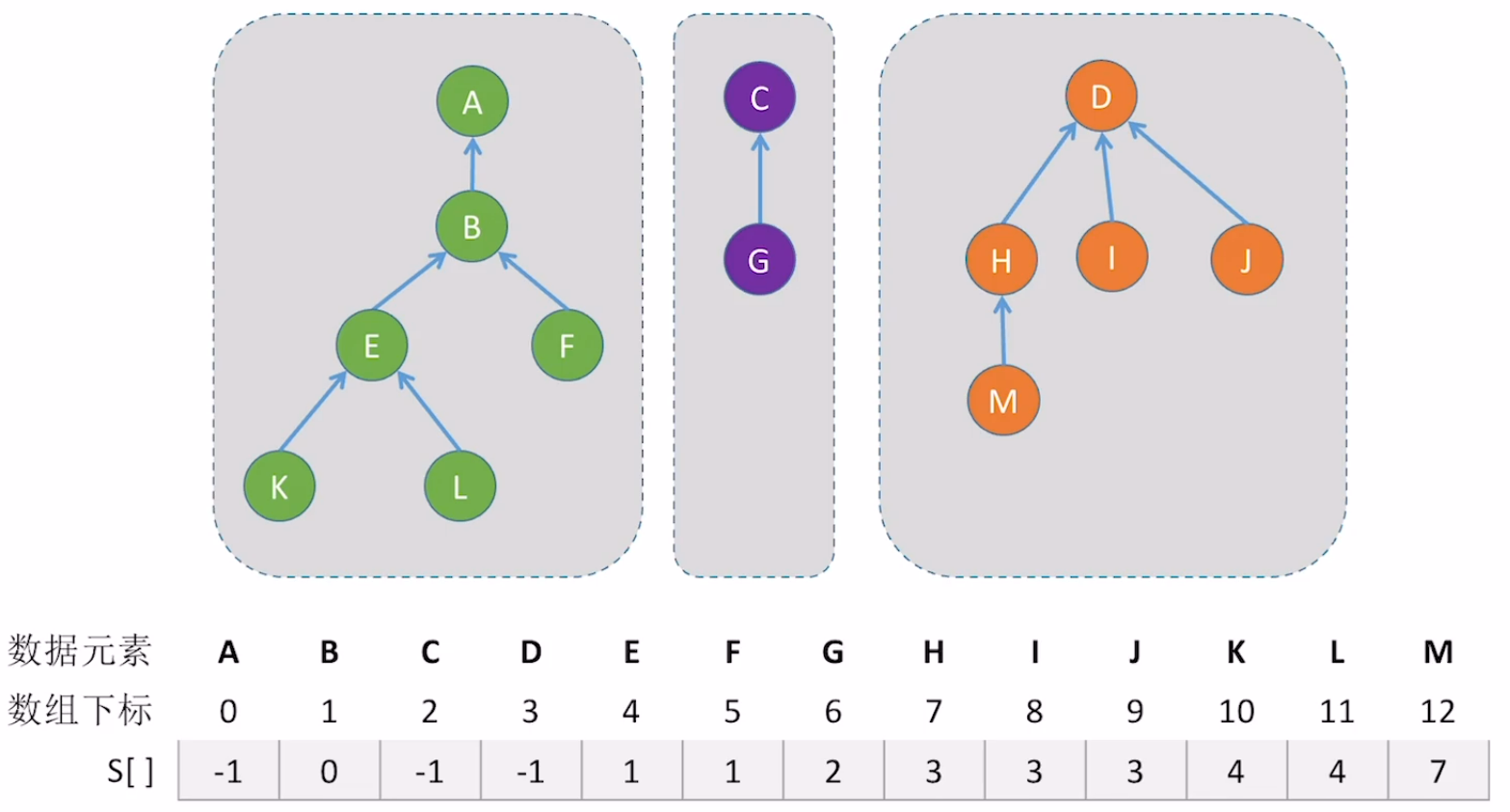
其中parent指针指向的结点。
集合初始化代码如下:
xxxxxxxxxx71int UFSets [SIZE];//集合元素数组3//初始化并查集4void Initial(int S[]){5 for(int i=0;i<SIZE;i++)6 S[i]=-1;7}将上面元素根结点都设置为-1表示每个元素当前都是一个独立的子集。之后可以根据业务的具体需求对元素进行合并操作。
1. 集合查操作
集合关于查的操作主要有以下两个:
- 给定一个元素
E如何查到这个元素所属集合:从指定元素出发一路向北,找到根节点即可。 - 如何判断两个元素是否属于同一集合:分别查到两个元素的根,判断根节点是否相同即可。
查找代码如下:
xxxxxxxxxx61//Find“查"操作,找x所属集合(返回x所属根结点)2int Find(int S[],int x){3 while(S[x]>=0) //循环寻找x的根4 x=S[x];5 return x; //根的S[]小于06}如我们要找到L元素所属集合:L的s[]的值为4,即所指元素为E;E的s[]的值为1,指向B;而B的s[]为0指向A,A的s[]为-1代表此为根元素,即L从属于A。
若结点数为
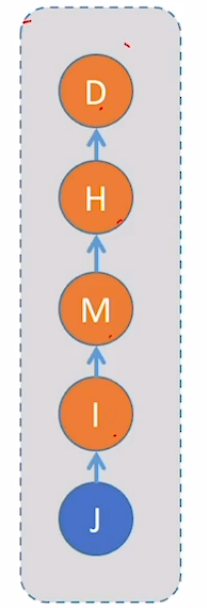
那么此时算法时间复杂度就增加,所以查找时间复杂度和树的高度
2. 集合的合并操作
合并两个集合操作:让一棵树成为另一棵树的子树即可。
合并集合代码如下:
xxxxxxxxxx71//Union “并"操作,将两个集合合并为一个2void Union(int S[], int Root1, int Root2) {3 //要求Root1与Root2是不同的集合4 if(Root1==Root2)return;5 //将根Root2连接到另一根Root1'下面6 S[Root2]=Root1;7}上面的Root1和Roor2代表要合并的两个树根结点的数组下标。
如果给定的元素不是根结点,那要查找两个元素的根结点,再进行合并操作。
3. 并查集的优化
若结点数为
优化合并算法可以降低查询算法的时间复杂度,优化思路是:
- 用根节点的绝对值表示树的结点总数
- Union操作, 让小树合并到大树
并查集存储结构:

可以优化为:

上面A所对应的s[]值为-6,代表树的结点为s[]的负值的绝对值代表了该树有多少结点。
合并优化后代码:
xxxxxxxxxx111//Union“并"操作,小树合并到大树2void Union(int S[],int Root1, int Root2) {3 if (Root1==Root2 ) return;4 if(S[Root2]>S[Root1]) { //Root2结 点数更少5 S[Root1] += S[Root2]; //累加结点总数6 S[Root2]=Root1; //小树合并到大树7 } else {8 S[Root2] += S[Root1]; //累加结点总数9 S[Root1]=Root2; //小树合并到大树10 }11}假设合并A和C两棵树,其对应的Root1=0,Root2=2;显然Root2>Root1即树A结点树大于树C。再执行S[Root2]=Root1;将小树合并到大树。合并后的树如下:

该算法优化后可以让树的高度不超过
4. 并查集优化2
可以类似与缓存那样,将Find查找的结点所经过路径的所有结点直接成为根结点的子结点。此时,可以让之后查找的路径变短,这种让查找路径变短的方法称为压缩路径。
如我们要找L结点所属集合,此时L结点查找必经过E和B结点:
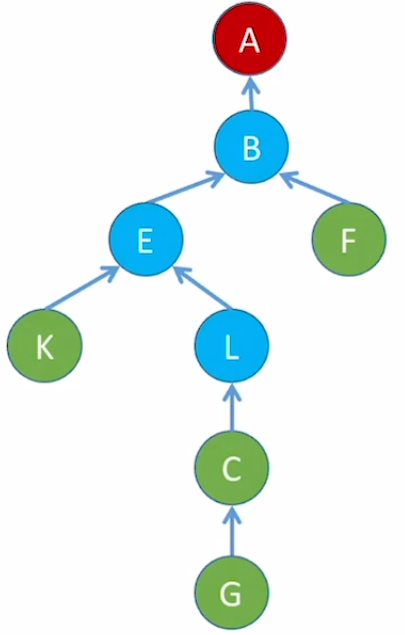
优化后树的结构图如下:
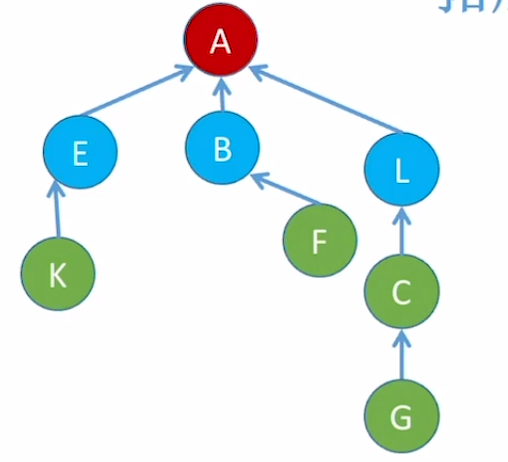
优化后树的存储结构如下:

压缩路径:Find操作,先找到根节点,再将查找路径上所有结点都挂到根结点下。
代码实现方式如下:
xxxxxxxxxx121//Find “查”操作优化,(先找到根节点再进行“压缩路径”2int Find(int S[],int x){3 int root = x;4 while(S[root]>=0)5 root=S[root]; //循环找到根6 while(x!=root){ //压缩路径7 int t=S[x]; //t指向x的父节点8 S[x]=root; //x直接挂到根节点下9 x=t;10 }11 return root; //返回根节点编号12}每次Find操作,先找根,再"压缩路径",可使树的高度不超过Find、Union操作时间可以用常数级时间复杂度