十三. 微分学与积分学应用
1. 一元函数微分学应用
1.1 物理应用
已知质点运动的位移关于时间的函数,称它为质点的运动方程(位移方程),则其速度为
其加速度为
常用关系式:,,
1.2 相关变化率
若函数均可导,则,上式中,与由联系在一起,称这种相互关系关联的变化率为相关变化率
已知动点在曲线上运动,记坐标原点与点间的距离为,若点的横坐标队时间的变化率为常数,则当点运动到点时,对时间的变化率是多少
1.3 几何应用
设二阶可导,则曲线在其上点处的曲率公式为
曲率半径计算公式
例曲线求在对应点处曲率 解:代入曲率公式 2. 一元函数积分学应用
2.1 变力沿直线做功
设方向沿轴正向的力函数为,则物体沿轴从点移动到点时,变力所做的功为
功的微元
变力沿直线做工:
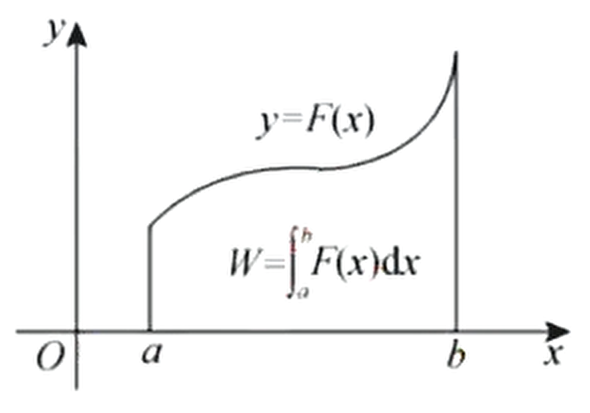
注意:力关于位移的定积分就是功
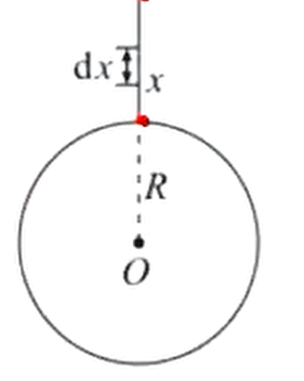
例设地球质量为,半径为,将地面上的质量为的物体举高米,求克服重力所作的功
解:如下图所示考虑将物体从距地心米处举高到距地心米情况在此过程中假设物体所受的重力大小近似为其中是引力常量将物体从距地心米处举高到距地心米时克服重力所做的功的微元为于是所求功为 做功例题:
2.2 抽水做功
如下图所示,将容器中的水全部抽出所做的功为
其中为水的密度,为重力加速度。功的微元为位于处厚度为,水平截面面积为的一层水被抽出(路程为)所做的功。
抽水所做的功:
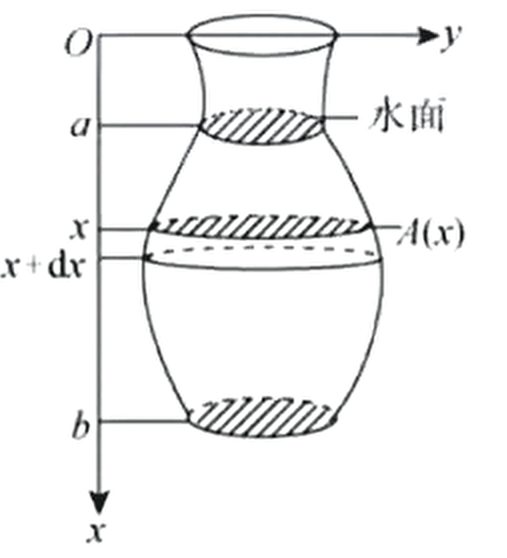
注:抽水所做的功特点:力(重力)不变,路程在变,求解这类问题关键是确定处水平截面面积,其余的量都是固定的。
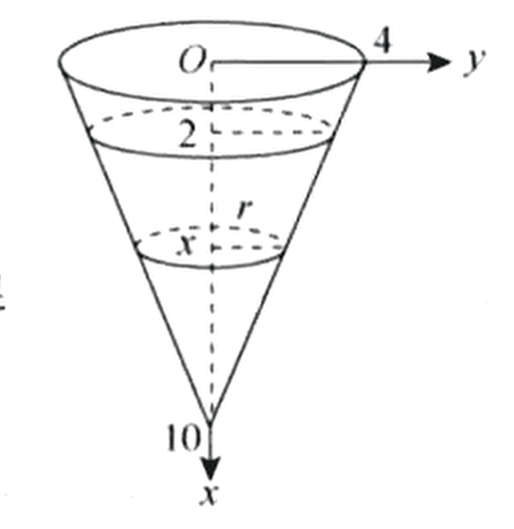
例有一倒圆锥形容器,高,上底半径,水面高,求将容器中的水全部从容器顶部抽出所做的功(水的密度为,重力加速度为)
解:如下图所示建立坐标系在处的水平截面半径满足即截面面积所以将水全部抽出所做功 抽水所做的功例题:
2.3 水压力
垂直浸没在水中的平板的一侧收到水压力为
其中为水的密度,为重力加速度。压力微元,即图中矩形条所受到的压力,表示水深。是矩形宽度,是矩形条的高度。
水压力:

注:水压力问题特点:压强随水的深度的改变而改变,求解这类问题关键是确定水深处的平板的宽度
例洒水车上的水箱是一个横放的椭圆柱体,椭圆的尺寸如下图所示,当水箱装满水时,计算水箱的一个端面所受的压力(水的密度为,重力加速度为)
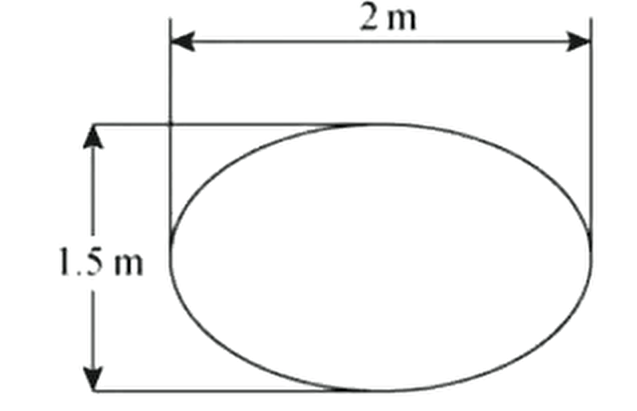
解:如下图所示建立坐标系在处椭圆的宽度为处的深度为所以椭圆所受到的压力 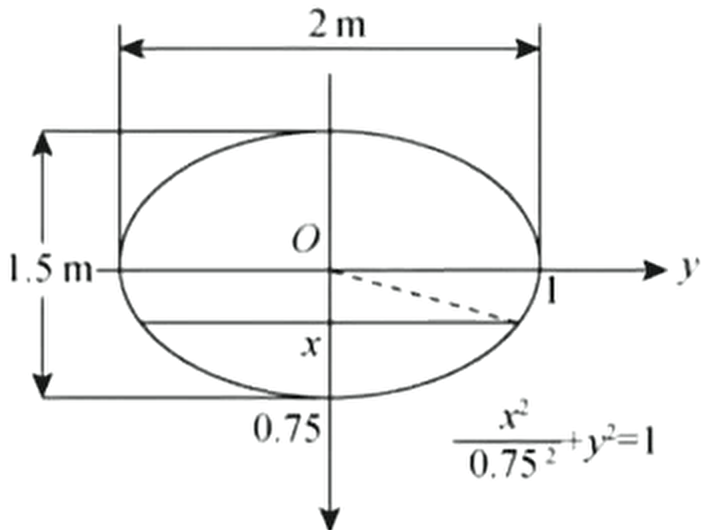
2.4 几何应用
"平面上的曲边梯形"的形心坐标公式
设平面区域在上连续,如下图所示,先推导的形心坐标的计算公式
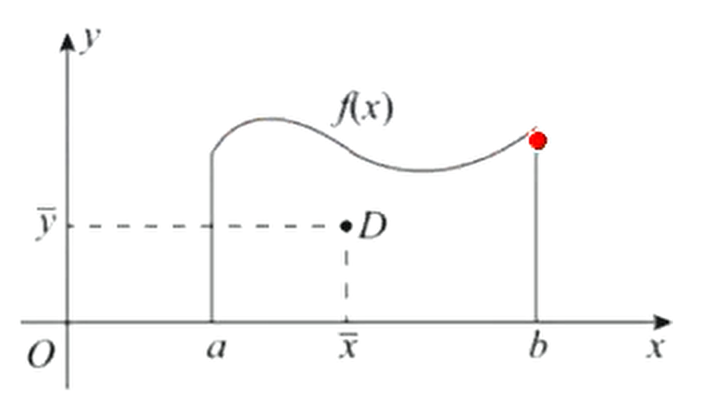
例设曲线的方程为,是曲线,直线及轴围成的平面图形,求的形心横坐标
解: 平面曲线的弧长
①若平面光滑曲线由直角坐标方程给出,则
②若平面光滑曲线由参数方程给出,则
③若平面光滑曲线由记坐标方程给出,则
例计算曲线上相应于的一段弧的长度
解:代入公式即可 例求心形线的全长,其中是常数
例求星形线的弧长
解:星形线具有对称性只用计算第一象限弧段即可 旋转曲面的表面积
①曲线在区间上的曲线弧段绕轴旋转一周所得的旋转曲面的表面积
解: ②曲线在区间上曲线弧段绕轴旋转一周所得到的旋转曲面表面积
例设有曲线,过原点作其切线,求此曲线、切线及轴围成的平面图形绕轴旋转一周所得到旋转体的表面积
解:设切点的横坐标为则切点为曲线在此点的切线斜率为于是切线方程为又因它经过原点将点代入得解得于是切线方程为即切点曲线段绕轴旋转一周所得到的旋转面的表面积为由直线段绕轴旋转一周所得到的旋转面的表面积为因此所求旋转体的表面积为 平行截面面积为已知的立体体积
在区间上,垂直于轴的平面截立体所得到得截面面积为得连续函数,则的体积为
3. 微分方程的物理应用
3.1 牛顿第二定律
相关物理量有:①物体质量;②力(包括重力、浮力、阻力);③加速度
例某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下。现有一质量为的飞机,着陆时的水平速度为,经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为)。问从着陆点算起,飞机滑行的最长距离是多少?(表示千克,表示千米时)
解:由题知阻力为故两边分离变量积分在时刻位移代入得故即当速度趋向于时可以达到最大距离即当时 3.2 变化率问题(1)
主要涉及:变化率、增长率、减少率、繁殖率等,且时刻某量对的变化率与时刻某量成正比反比。一定要理解这句话。
如:对的变化率与时刻某量成正比,即,还要分析与变化大小判断是否加负号。
注意:
- 题中正比例关系为:,随增大而增大。,随增大而减小。
- 反比例关系:,随增大而增大。,随增大而减小。
解题步骤:
- 设目标函数;(可分离变量型微分方程,也即题中变化率),其中是因变量,是自变量。
- 依题意列出偏导关系,并找出题目初始条件;
- 解方程即可
例题根据冷却定律知,物体在空气中的冷却速度与物体温度和空气温度之差成正比,一个装有100°C热水的水瓶,加上盖,放在20°C的环境温度中冷却, 在24小时后,测量温度为60°C,求水瓶中水温下降的函数表达式。
解:设水温下降函数为为时间由题可知冷却速度其中初始条件两侧积分由得 例题:在某池塘内养鱼,该池塘最多能养尾,在时刻,鱼数是时间的函数,其变化率与鱼数及之积成正比。已知在池塘内放养鱼尾,3个月后池塘内有鱼250尾,求放养月后池塘内鱼数的函数。
解:设变化率函数变化率为初始条件由得 例题某文物与1972年8月发掘出土,经研究测算该文物出土时放射性同位素碳十四标本存量为初始量的倍。已知的衰变速度与他的现存量成正比,且它的半衰期由初始量衰变至所需要时间为5740年。
试求的现存量与时间年的函数关系(其中对数不必写出具体数值)。
计算该文物至1972年8月大约经历了多少年,能否认为该文物为西汉时期(公元前202公园8年)的作品并说明理由。(计算结果取整数;其中).
解:令现存量为其与时间有函数关系为且衰变速度与他的现存量成正比随着变大减小分离变量积分解得由题可知当时现存量为初始量且半衰期为年由得 解:该文物出土时放射性同位素碳十四标本存量为初始量的倍解得因此文物存在了年大约出现在公元前年该文物为西周文物 总结:
应用题还是要具体问题具体分析,可分离变量微分方程应用题还是要找到变化率与某刻变化量比例关系,前者比例关系倍的后者。特别是要体会那个与字前后变量关系。其本质也就是找到因变量变化率和自变量变化量之间的关系,与这样的一元函数变量关系实际上没有区别,只不过变为了为的自变量。
当然还要找到题中两个初始量求出比例常数和分离变量后常数。题中可能隐藏时刻初始量,读者自行判别。
3.3 变化率问题(2)
设总人数为,时刻已掌握新技术的人数的变化率和已掌握新技术与未掌握新技术的人数之积成正比。此时表达式应写为:正号代表(人数随着时间增加而增加)。
4. 欧拉方程
形如的方程称为欧拉方程,其中与为常数,为已知连续函数。它有固定解法。
(1)当时,令,则,,于是
原方程化为:
(2)当时,令
例求欧拉方程的通解
解:令原方程变为即特征方程 5. 傅里叶级数
设以为周期的函数在上①连续或只有有限个第一类间断点,②且至多只有有限个(真正的)极值点,则的傅里叶级数处处收敛,记其和函数为,则有
称这个为三角级数或傅里叶级数,由于以为周期,则系数表达式为:
5.1 正弦级数和余弦级数
若为奇函数,则
此时展开:
由于级数中只有,所以称为正弦级数。
若为偶函数,
展开为:
由于级数中只有,所以称为余弦级数。
5.2 奇延拓与偶延拓
若在上,将图形关于原点在上作出对称图形,使其变为在上奇函数,此时称为奇延拓。
即令 这里注意情况,若原先函数,只能修改此处定义,强行令,以保证在上为奇函数。
奇延拓:
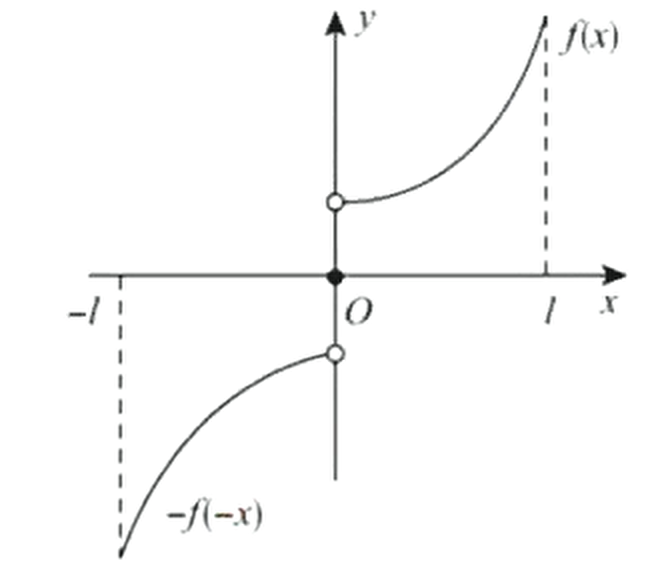
若在上,将图形关于轴在上作出对称图形,使其变为在上偶函数,此时称为偶延拓。
即令 偶延拓:
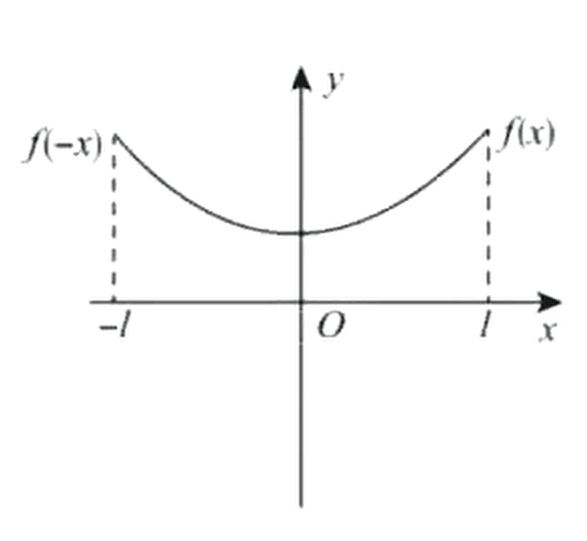
例将函数展开成余弦级数,并求
解:由于余弦函数为偶函数展开故作偶延拓展开其中将代入当时即故 5.3 狄利克雷收敛性定理
前面写的在上展开为,或写为,之所以为是因为并不一定等于。这里在什么情况下等于,什么情况下不等于就用到了狄利克雷收敛性定理。定理如下:
为连续点为第一间断点间断点左极限间断点右极限左端点右极限右端点左极限 例设其中求 解:图形如其偶延拓图形如周期为偶函数由狄利克雷收敛性定理 5.3-1:
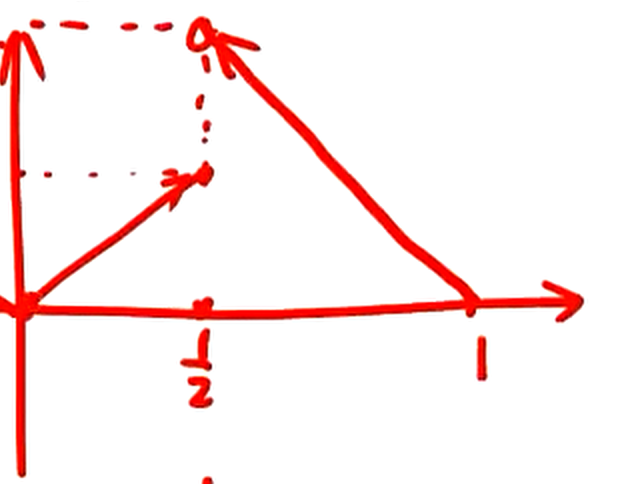
5.3-2:
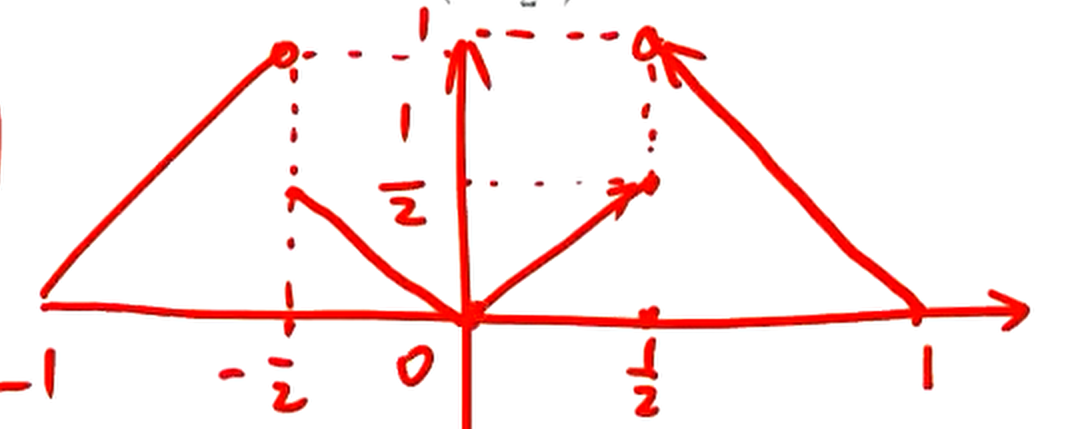
十四. 向量代数
既有大小又有方向的量称为向量。向量表达式:
空间对称:求对称点方法:关于字母对称,哪个字母不变,其他字母变负。如:关于原点对称点为关于对称点为
向量的表示:
坐标表示若则 向量表示其中是轴方向的单位向量是轴方向的单位向量是轴方向的单位向量 1. 向量的模和方向余弦
向量的模(大小):就是向量到原点的距离。公式:
向量的单位化:向量的方向不变,模长化为。公式:
方向余弦:向量与坐标轴方向的夹角,有三个,它们分别是与方向的夹角余弦值。公式:
要求:只能在范围内。并且同一方向上
2. 向量的运算
2.1 向量的线性运算
向量的线性运算(加减数乘):设
,数乘后的向量和原向量成平行关系与原向量共线
向量的加减法几何意义
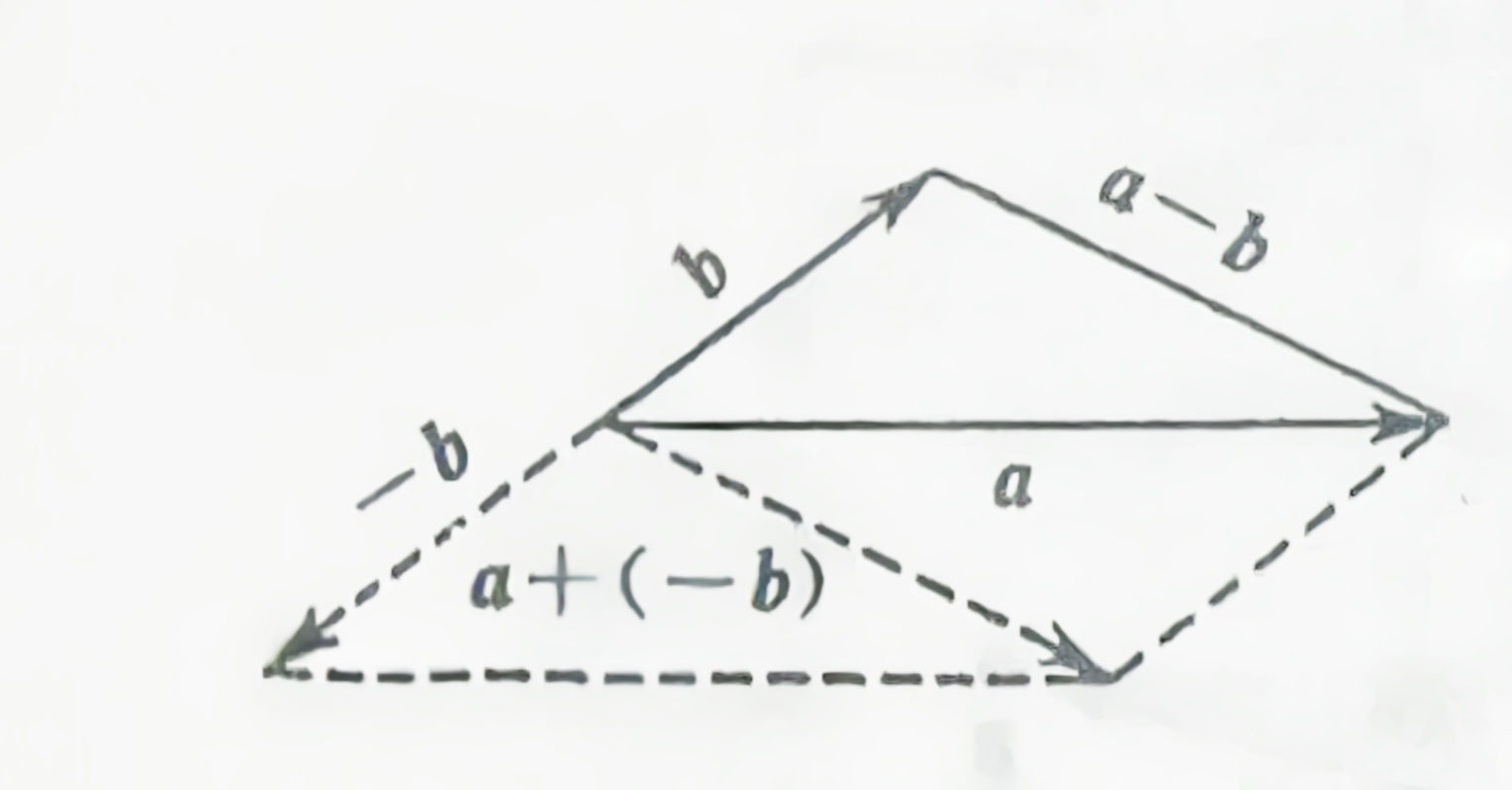
向量的加减可以借助三角形法则和平行四边形法则
向量的加法:
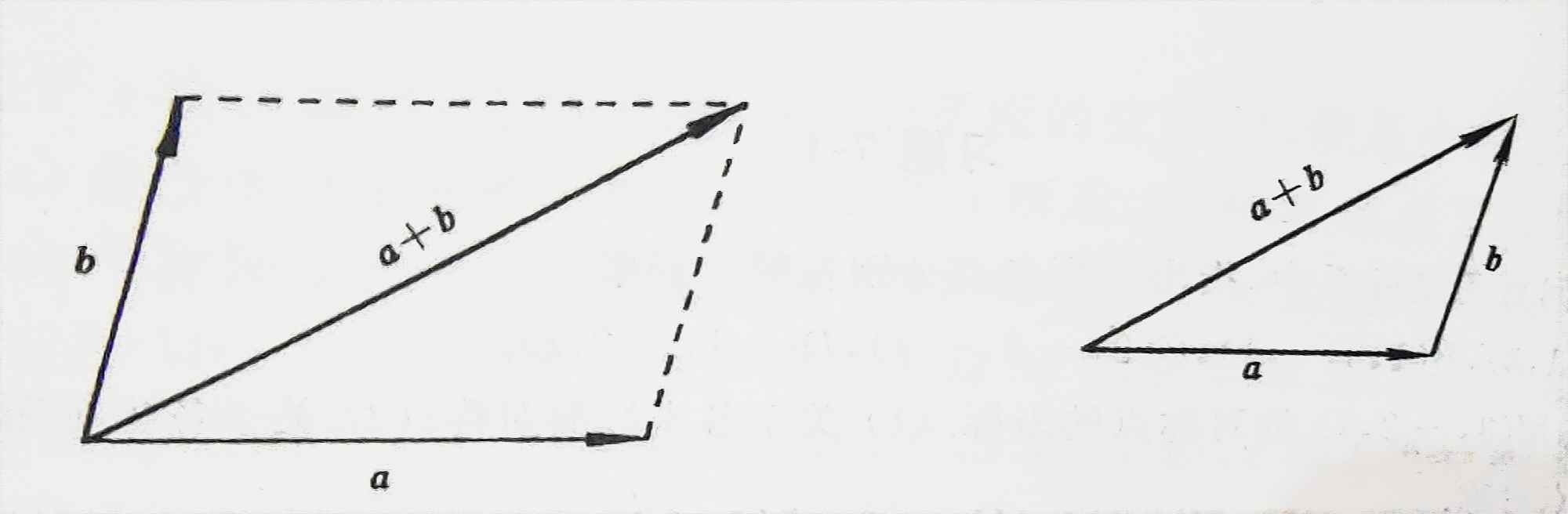
由向量的加法可以突出向量减法
向量的减法:
[ ](
](
2.2 向量的乘(点乘和叉乘)
例已知求
解:由三角形即共起点向量叉乘的一半可得 3. 向量的投影
在的投影和在的投影
在谁上投影就除以谁的模长在上的投影:在上的投影: 4. 向量的位置关系
位置关系分两种:平行、相交(斜交和垂直)
方法:
- 先看对应坐标是否成比例,如果成比例,则平行
- 如果两个向量点乘等于,则两向量垂直
- 既不平行也不垂直则为斜交,斜交度数:且
5. 空间平面与直线
5.1 平面方程
知道平面上的任意一点和法向量就能写出平面方程。法向量
①点法式方程:
②将上面的点法式方程展开得一般式
③三点式:
平面过不共线的三点 ④截距式:(平面过三点)
判断用点法式还是一般式
条件:若题中已知过原点,平行轴平行面,用一般式方程,其他情况都用点法式方程。
过原点情况下,平行轴(面),平行于哪个字母,哪个字母前系数等于。如:平行,则
过轴:先平行于哪个字母,哪个字母前系数等于再,如:过,则
5.2 直线方程
①一般式方程:空间直线可以看作两个空间平面的交线,设两个平面分别为与,则称联立方程组,为空间直线的一般式方程:
空间直线的方向向量为,
②点向式方程为:把平行于直线的非零向量称为直线的方向向量,并记,设直线过一定点,则直线的点向式方程为:
③直线的参数方程:设,其中为参数,则参数方程:
其中前的系数是方向向量。
④两点式:(直线过不同的两点)
6. 平面与直线位置关系
6.1 平面的位置关系
平面的位置关系本质就是它们法向量的位置关系。所以只要找到两个平面的法向量,就能确定它们的位置关系。
注:两平面的夹角范围值
6.2 直线的位置关系
两个直线的位置关系就是他们方向向量的位置关系
注:两直线的夹角范围值
6.3 直线与平面的位置关系
直线与平面的位置关系和方向向量与法线的位置关系相差。即:设方向向量和法向量
例求直线和平面的位置关系
解:由题可知方向向量与不成比例不平行于不垂直不垂直于不平行于此时斜交 7. 距离公式
7.1 点到点间的距离公式
设点,点
则点到点间的距离公式为:
7.2 点到平面的距离公式
点到平面的距离公式:
即点代入平面的绝对值平面法向量的模长 例点到平面的距离
解: 7.3 两平行平面的距离
平面平面,此时距离公式为:
在计算距离之前要先把和的法向量化为一致。
例两平面平行,求两平面距离
解:先将两平面法向量化为一致即两边同除此时法向量 7.4 点到空间直线的距离
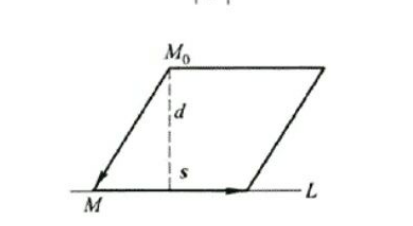
设是直线外一点,是直线上任意一点,且直线的方向向量为,则点到直线的距离:
以上都为取模长
证明:如下图所示,点到直线的距离为,由向量积的几何意义知表示的是以为邻边的平行四边形的面积而距离公式表示以为边长的该平行四边形的高即为点到直线的距离于是 点到空间直线距离证明:
例点到空间直线的距离
解:由题可知平面上的一点方向向量为则 7.5 点在平面或直线上的投影
思路:先求出过该点并且和直线平面垂直的平面方程直线方程。之后联立方程求出其交点即可。
例求点在平面的投影点坐标
解:设点过点垂直于平面直线方程为将直线方程化为参数方程将参数方程带入平面方程为从而得坐标点为 例求点在直线上的投影点坐标
解:设点由直线的参数方程可得方向向量由于平面和直线垂直可知方向向量法向量可知平面方程将代入平面方程可得从而投影点坐标为 8. 空间曲线
8.1 判断空间曲线
空间曲线的一般方程:
其几何背景为两个曲面交线 参数方程:
考点:判断空间曲线是什么样的曲线
方法:
- 化简空间曲线的方程组(消元),化简前后方程组中变量个数不变。
- 看化简后的方程组,其中复杂的方程在二维中表示什么曲线,则在三维中就表示什么曲线。
例方程组表示的是什么曲线 解:化简两式相减解的代入方程组其中一个此时可以看出方程组中较为复杂方程是一个圆则在三维中也是圆 8.2 空间曲线在坐标中的投影
空间曲线关于坐标面投影的柱面方程(二元方程)
- 情况一:母线平行于哪个坐标轴就把对应的变量消去
- 情况二:求关于哪个坐标平面的投影柱面,就把它另外的变量消去
空间曲线在坐标面投影的曲线方程(方程组)
- 方程组中的一个是投影柱面方程(二元方程)
- 方程组中的第二个是坐标面方程。如:投影
例求曲线在平面投影的曲线方程 解:方程为投影柱面方程投影关于平面投影我们消得投影柱面方程可得投影柱面方程由此可得曲线方程空间曲面 9. 空间曲面
9.1 空间曲面方程特征
空间曲面方程特征:
三元全二次:椭球、球面、双曲面、圆锥面三元二次一次:抛物面二元方程:平面或柱面方程两个就是平面一个则为柱面旋转曲面:平方项系数至少有个相同注意:在判断时先把平方项移至等式一边。 柱面在二维中是什么,三位中就是什么柱面。如:在二维中是圆在三维中就是圆柱面
旋转曲面举例:
9.2 空间曲面几何图形
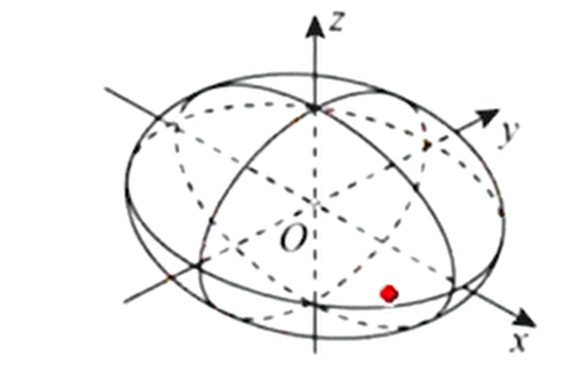
椭球面:,特殊:
椭球面:
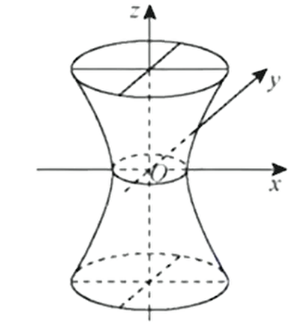
单页双曲面:
单叶双曲面:
双叶双曲面:
双叶双曲面:
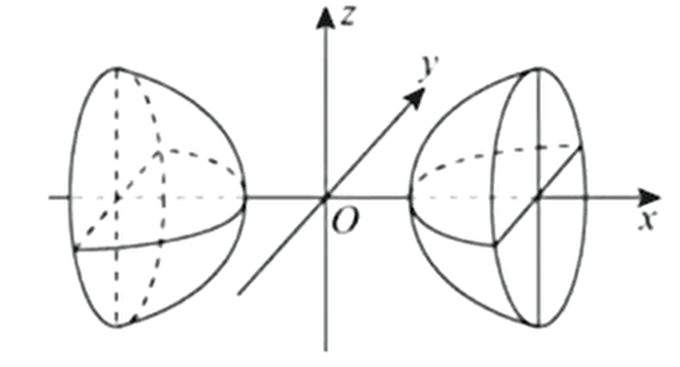
椭圆抛物面:,旋转抛物面:
椭圆抛物面:
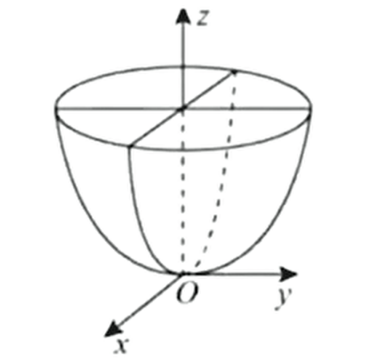
椭圆锥面:,特殊方程:,锥面:几何图形之有上半部分
椭圆锥面:
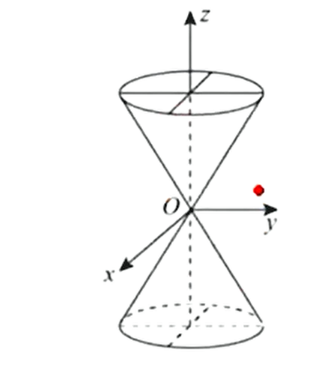
双曲抛物面(马鞍面):,特殊:
马鞍面1:
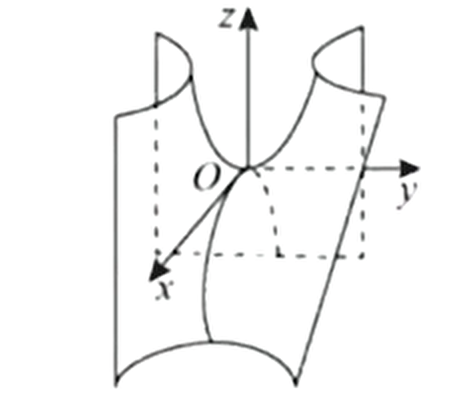
马鞍面:
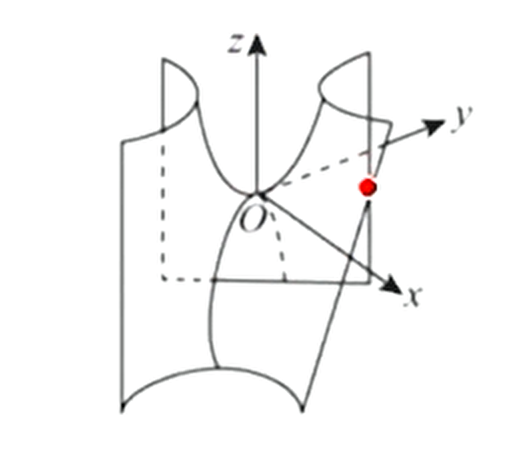
椭圆柱面:(当时为圆柱面)
椭圆柱面:
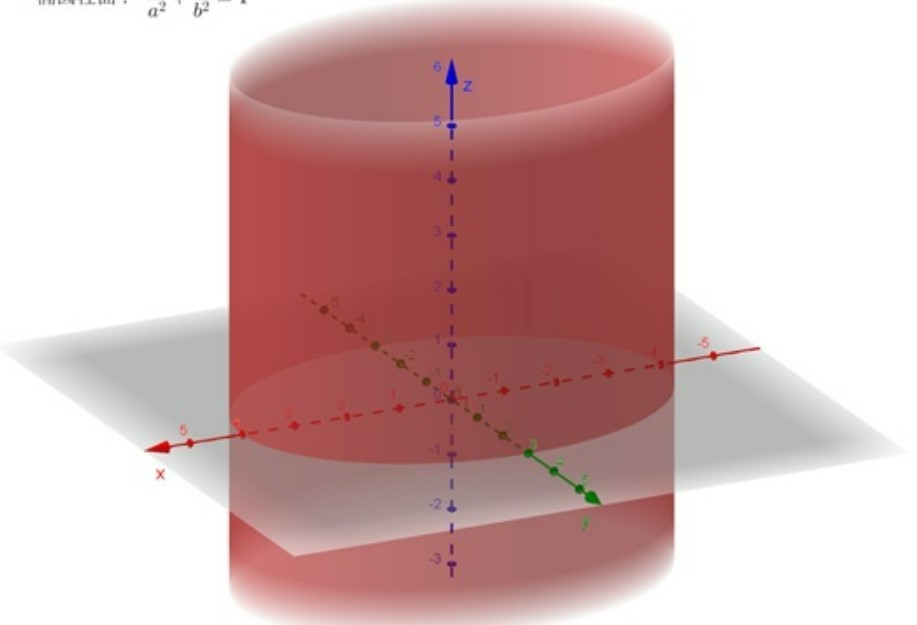
双曲柱面:
双曲柱面:
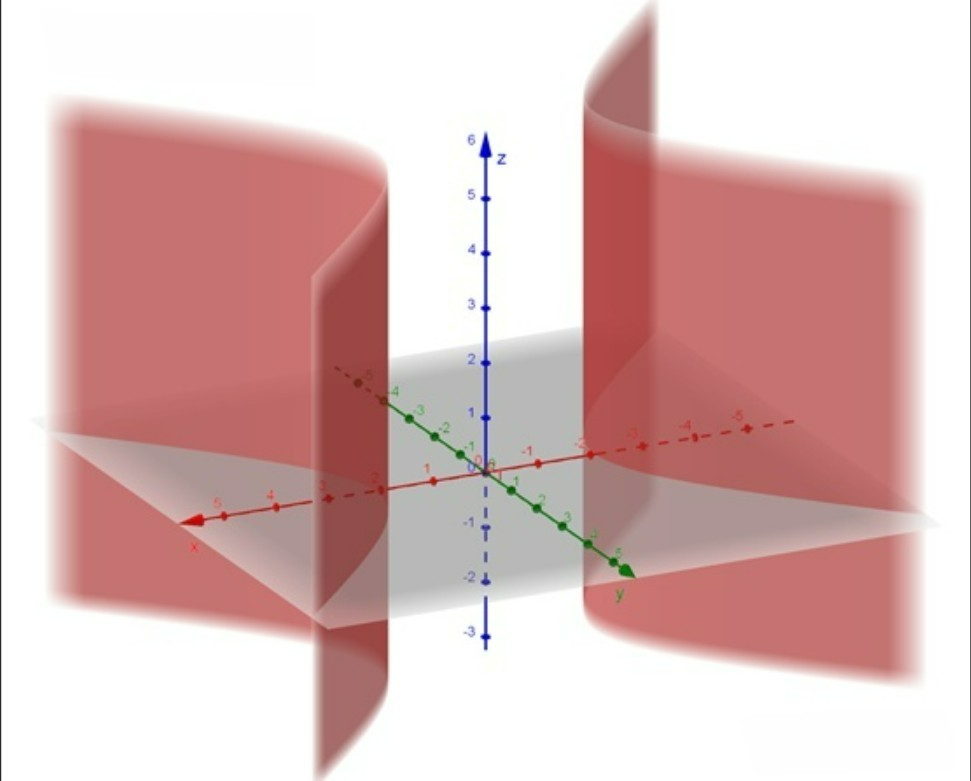
抛物柱面:
抛物柱面:
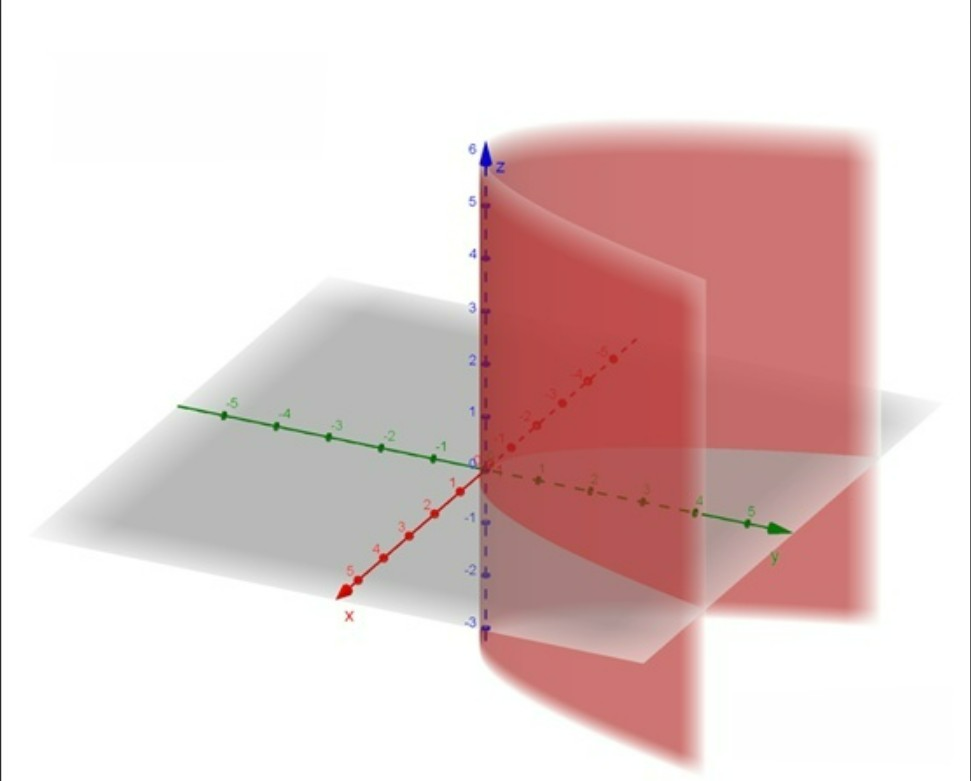
10. 旋转曲面求法
(1)旋转曲面:曲线绕一条定直线旋转一周所形成的曲面。曲线绕直线旋转形成一个旋转曲面,旋转曲面方程求法如下:
如下图所示,已知点,方向向量在母线上任取一点,则过的圆上任意一点满足条件:,
旋转曲面:
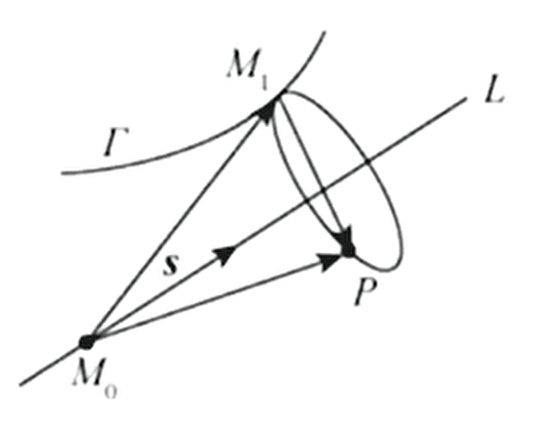
即
与方程和联立消去便可得到旋转曲面的方程。
例求直线绕轴旋转一周所形成的曲面方程
解:设直线上一点为直线绕轴转则经过原点且轴方向向量过的圆上任意一点满足条件故点消去代入得 (2)旋转曲线一个参量为,且绕某一坐标轴旋转情况,形如:
方法:绕谁旋转谁不变,另一变量变成该变量与第三变量平方和的正负平方根。
如:绕轴旋转所得旋转曲面方程:。绕轴旋转所得旋转曲面方程:
求:双曲线绕轴旋转所得旋转曲面 解:绕轴旋转方程绕轴旋转方程 11. 多元函数微分学的应用
可以分为:
空间直线(切线和法线):使用的是点向式,关键是方向向量\overrightarrow{s}
空间平面(法平面和切平面):使用的是点法式,关键是法向量\overrightarrow{n}
无论是法向量还是方向向量,其再多元函数中都是一样的,都是多元函数在具体点处的三个偏导数。即是方向向量又是法向量。
注意:曲线用参数方程,曲面用隐函数。
11.1 空间曲线的切线与法平面
空间曲线的切线:对应空间直线(点向式)
空间曲线的法平面:对应空间平面(点法式)
(1)设空间曲线由参数方程,其中均可导,是上对应的点,且当时,都不为,则
①曲线在点处的切向量为
②曲线在点处的切线方程为
③曲线在点处的法平面(过点且与切线垂直的平面)方程为
(2)设空间曲线由交面式方程给出,则在以下表达式有意义的条件下,有
①曲线在点处的切向量为
②曲线在点处的切线方程为
③曲线在点处的法平面方程为
例求螺旋线在对应于点处的切线与法平面方程
解:,,当时,对应的切向量为;将点代入螺旋线方程的点于是切线方程为:法平面方程为:即: 11.2 曲面的切平面与法线
切平面:点法式方程
法线:点向式
(1)设空间曲面由隐式方程给出,可微,是上的点,则
①曲面在点处的法向量(垂直于该点切平面的向量)为
且法线方程为
②曲面在点处的切平面方程为
(2)设空间曲面由显式方程给出,可微,令是上的点,则
①曲面在点处的法向量为
且法线方程为
②曲面在点处的切平面方程为
若用表示曲面在点处的法向量的方向角,并假定法向量的方向是向上的,即它与轴正向所成的角是锐角,则法向量的方向余弦为
其中,
例在曲面上求一点,使该点处的法线垂直于平面,并求在该点处的法线
解:设所求的点为令故法向量法线垂直于平面故法线的方向向量平行平面法向量又由向量平行的充分必要条件有即代入曲面方程中得所求得点为则法向量法线方程为 例设直线在平面上,而平面与曲面相切于点,求
解:令则为平面法向量故其平面方程为即①由直线方程得将其代入①因而得解得 12. 场论初步
12.1 方向导数
定理(方向导数得计算公式):设三元函数在点处可微分,则在点处沿任一方向得方向导数都存在,且
二元函数同理,求方向导数步骤:
- 先求一般为题中两点的向量坐标:
- 求方向余弦、
例求函数在点处沿从点到点方向的方向导数
解:且的方向就是所求方向导数的方向所求方向导数为 12.2 梯度
梯度是偏导数的向量,设三元函数在点处具有一阶偏导数,则梯度公式:
梯度的意义就是沿着一个方向前进的快慢,即变化率。
方向导数最大值是梯度的模,最小值为梯度模的负数。即
补充:两梯度夹角计算:求出两个函数在两点处的梯度后代入:
求出的就是两个梯度的夹角。
12.3 方向导数和梯度关系
通过对比方向导数和梯度公式:
方向导数梯度 可知
其中为与的夹角,当时,有最大值。
结论:函数在某点的梯度是一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
12.4 散度和旋度
设向量场,则
散度:
旋度:
例求向量场在点处散度
解:由题可知 例设,求
解:故 十五. 三重积分
三重积分的区域由平面变为三维立体实心区域。三重积分表示为:假设在上可积,则
为体积。
1. 三重积分性质
性质1(求空间区域的体积):为体积
性质2(可积函数必有界):设在上可积,则其在上必有界
性质3(积分的线性性质):设为常数,则
性质4(积分的可加性):设在上可积,且,,则
性质5(积分的保号性):设在上可积,且在上,则有
特殊地,有
性质6(三重积分的估值定理):设分别是在上的最大值和最小值,为的体积,则有
性质7(三重积分的中值定理):设在上连续,为的体积,则在上至少存在一点,使得
2. 普通对称性与轮换对称性
分析方法与二重积分完全一致
(1)普通对称性
假设关于面对称,则
其中是在面前面的部分,关于其他坐标面对称情况与此类似。
例计算,其中
解:由于区域关于面对称且当故即为上半球实心区域 (2)轮换对称性
若把与对调后不变,则,这就是轮换对称性。其他情况类似
如,则可以化简计算。
例设,求
解:由于令令故 3. 三重积分计算
3.1 直角坐标系
(1)先一后二法(先后法,也叫投影穿线法)
使用场景:有下曲面,上曲面,无侧面或侧面为柱面,如下图所示:
先一后二法:
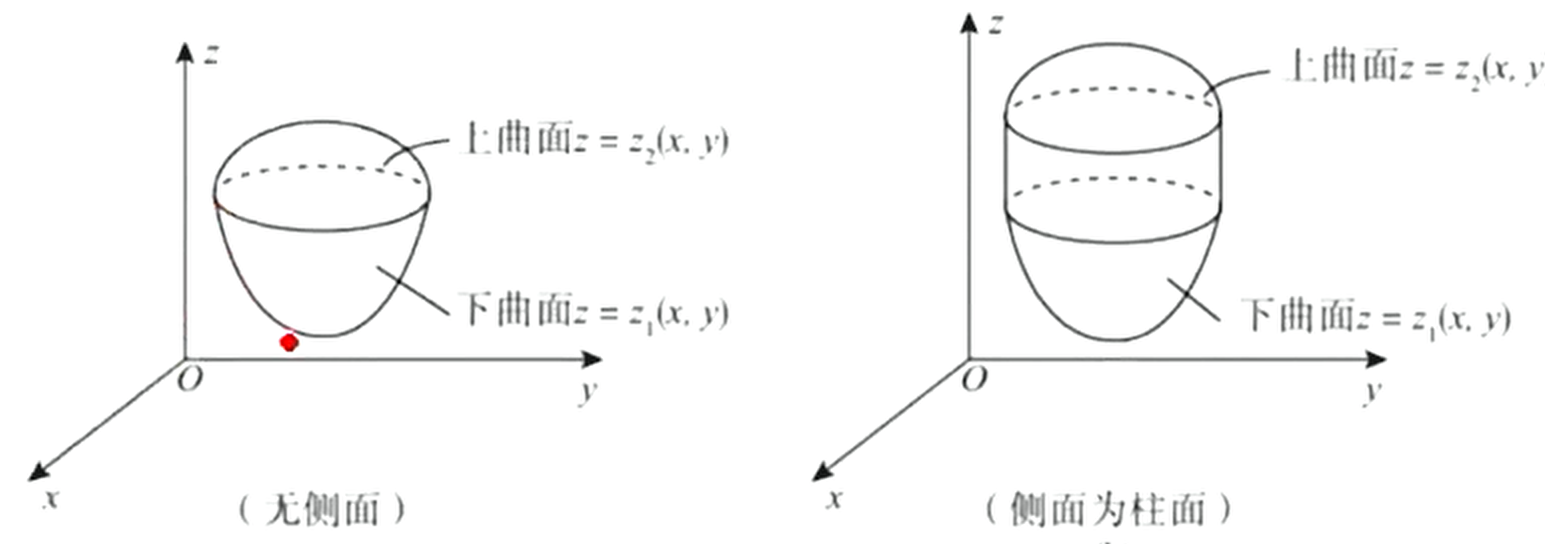
计算方法:将区域投影下来,如下图:
投影:
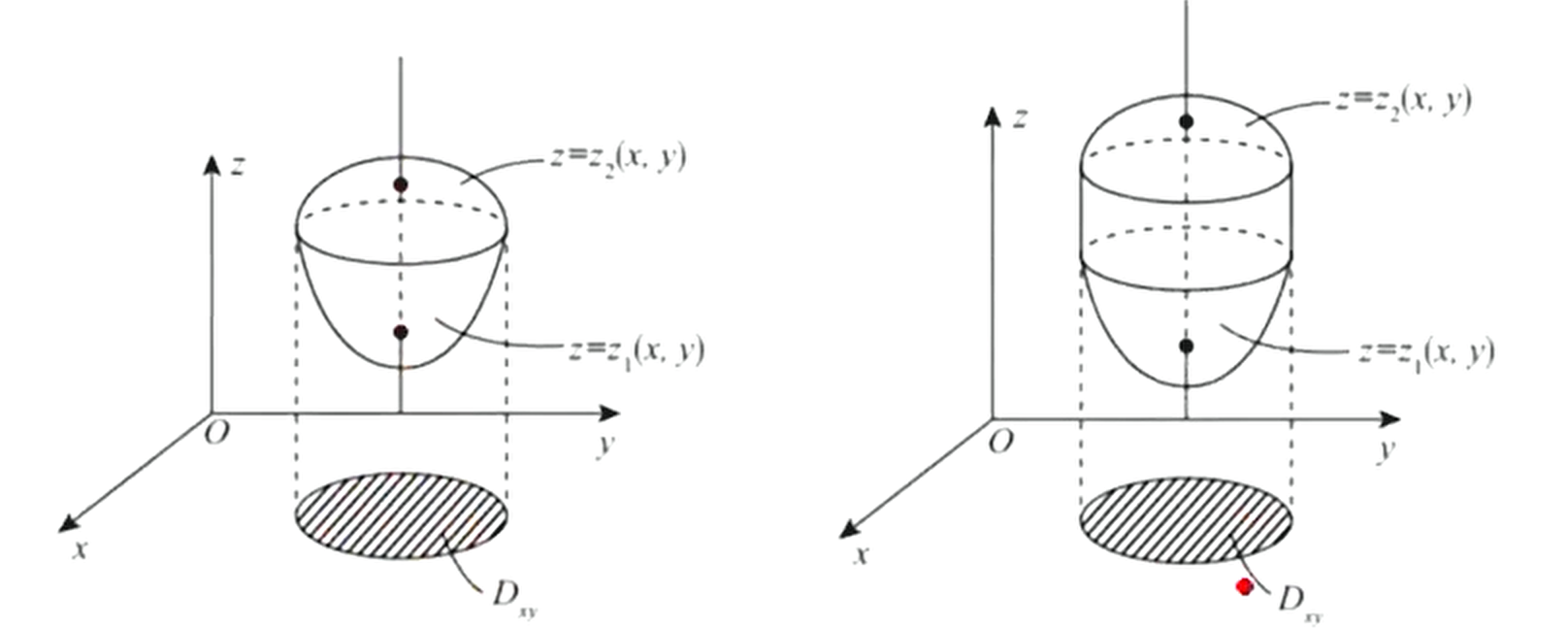
则有
例计算三重积分,其中是由平面及所围成的四面体
解:区域如下所示则 区域:
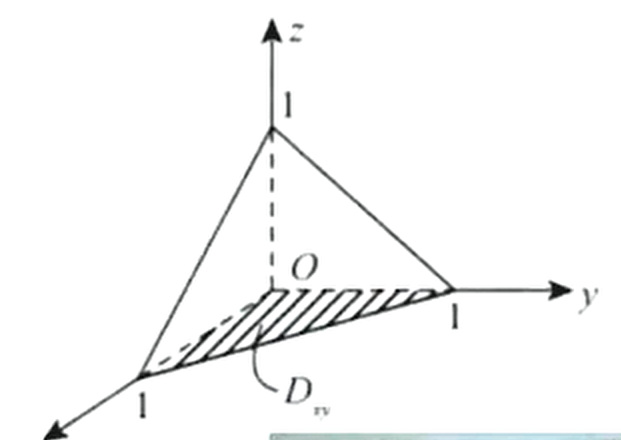
区域在投影图:
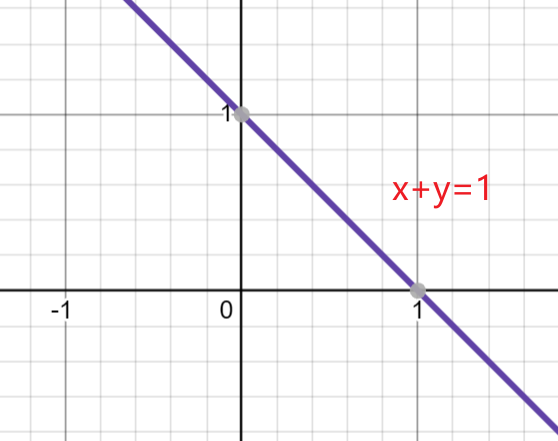
(2)先二后一法(先后法,也叫定限截面法)
①适用场合:是旋转体,其旋转曲面方程为,若函数,则更为方便。图形如下所示
先二后一法:
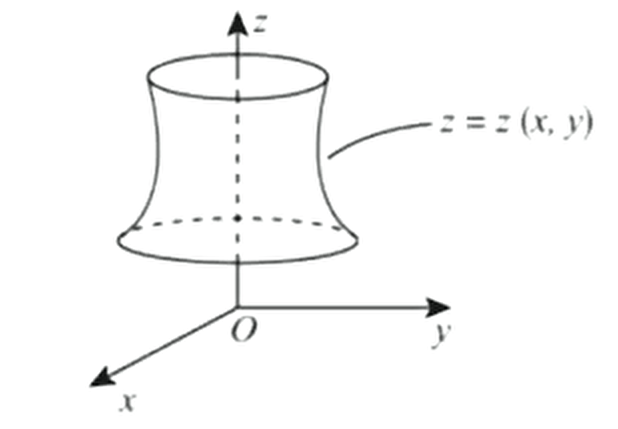
②计算方法:
先二后一法投影:
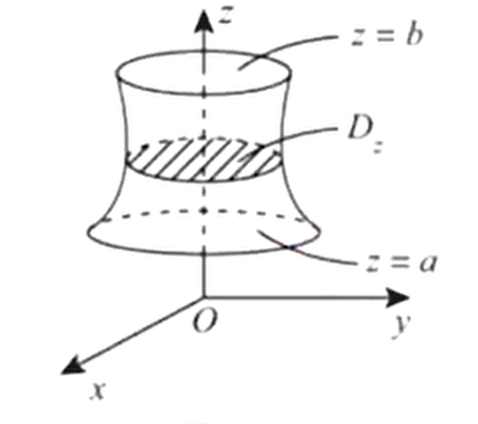
例计算,其中
解:由于区域关于面对称且当故即为上半球实心区域截面 3.2 柱面坐标系
适用场景:①投影是圆或是圆的部分②被积函数为其中之一与复合,如:.
柱面坐标系本质是:定积分极坐标系下的二重积分结构
计算:同样用先一后二法或先二后一法
例计算,其中为平面曲线绕轴旋转一周形成的曲面与平面所围成的区域
解:在上找一点设原点为绕轴旋转形成纬圆纬圆上取一点由于即①且轴方向向量故②又在曲线内故③联立①②③消去旋转曲面方程 3.3 球面坐标系
适用场合:①被积函数中含有.②积分区域为:球或球的部分,锥或锥的部分
计算方法:
令 用三族面将空间切分成一个一个微元体
其中:①常数,为球心在原点的球面,其半径为,这里,即从原点射线交曲线半径大小
②常数,为以轴正向中心轴的圆锥面,其顶点为原点,半顶角为,,即从轴区域从上到下转过角度
③常数,为过轴的半平面,其与面正向夹角为,,即从轴区域逆时针转一圈角度。
且:,即
例计算三重积分,其中是右半球面与面所围成的区域
解:其中被积函数故 4. 技巧总结
①对称性(包括普通对称性和轮换对称性)可以有效简化积分
②形心公式的逆用(由)其中为的体积
例设,求
解:由于令令故 十六. 曲线积分
1. 第一型曲线积分(对弧长的曲线积分)
弧长的曲线积分指的是:函数之间一段弧长没有方向l(没有方向)
如果曲线弧L是闭曲线,则函数f(x,y)在闭曲线L上对弧长的曲线积分记作
1.1 对弧长的曲线积分性质
性质一:
性质二:设为常数,则
性质三:设可分成两段光滑曲线弧和,即,则
性质四(曲线积分中值定理):设在在上连续,为的长度,则在上至少存在一点,使得
性质六(可积函数必有界):设在上可积,则其在上必有界
性质七(积分的保号性):设在上可积,且在上,则有
特殊地,有
性质八(空间曲线长度(弧长)):,其中为的长度
1.2 对弧长曲线积分的解法
对于曲线积分的计算方法是化为定积分后进行计算,下面就曲线弧的方程不同表示形式,讨论的计算方法。
曲线弧的方程为:
其中,和在上具有一阶连续导数,且。由弧微分公式可知:
1.3 第一类曲线积分对称性
(1)普通对称性
假设关于面对称,则
其中是在面前面的部分,关于其他坐标面对称情况与此类似。
例计算,其中为球面与平面的交线
解:由曲线积分对称性可知原积分令则故 (2)轮换对称性
曲线积分满足的轮换对称性:积分曲线为,如果将函数中的换成后,仍满足,那么在这个曲线上的积分满足关系式:
设是面上的一条光滑或分段光滑的曲线弧,对坐标具有轮换对称性,在上连续,则:
例设空间曲线的方程为,求
解:由曲线积分轮换对称性故由于故 2. 第一型曲面积分
其性质和第一型曲线积分相同,注意以下性质:
求空间曲面面积:,其中为面积
对称性也和第一型曲线积分相同,下面介绍第一型曲面积分计算:
本质是化为二重积分再计算。设曲面方程为,区域为曲面投影区域。则曲面积分:
区域投影在面上,此时
区域投影在面上,此时
区域投影在面上,此时
例设为曲面介于与之间的部分,求第一型曲面积分
解:图形如下其在上投影为圆环圆环区域故 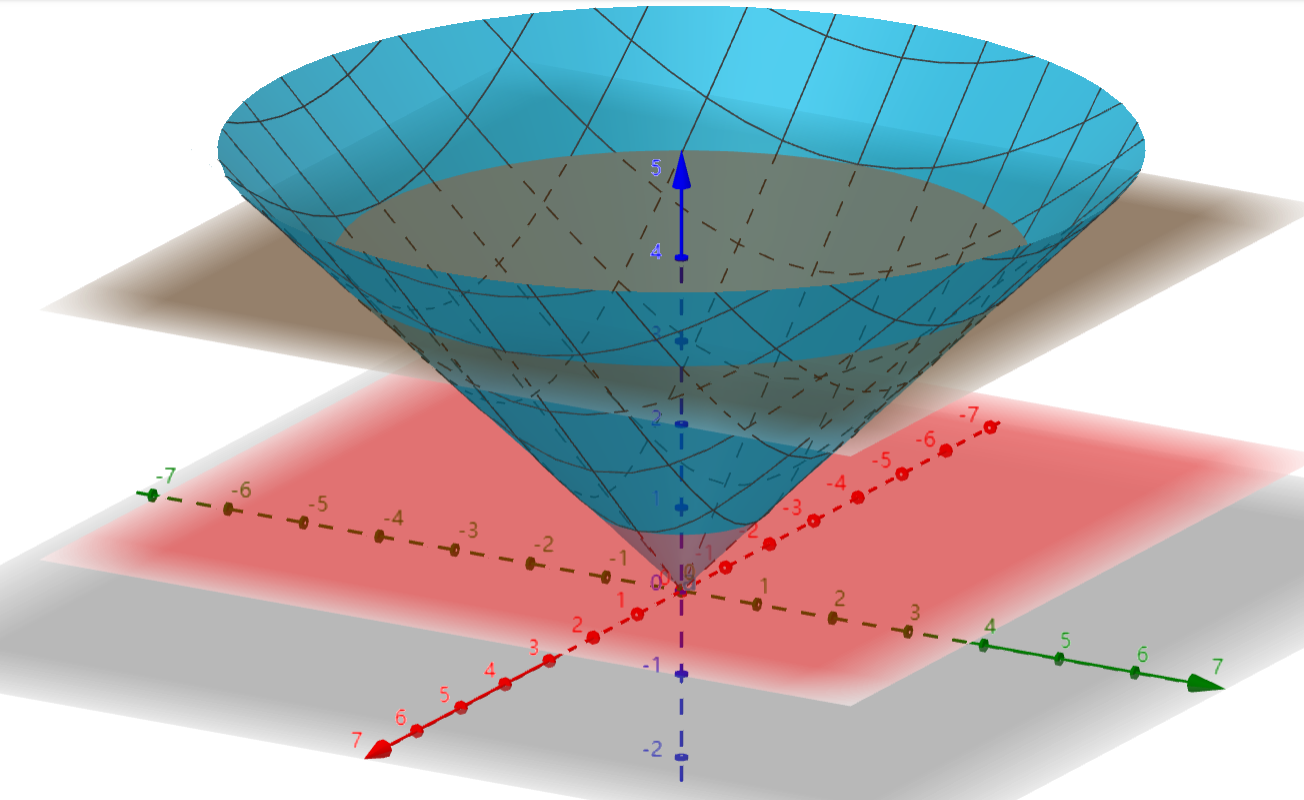
3. 第一型线面积分应用
3.1 几何应用
(1)对于平面区域有以下两种情况:
- 若是由与轴围成的曲边梯形,则其面积为,其中
- 平面区域的面积为
(2)对于空间区域,有两种情况:
- 以区域为底,曲面为顶的曲顶柱体的体积为
- 若是物体所占的空间区域,则其体积为
(3)对于空间光滑曲线,若其由参数,则计算空间曲线的长度(弧长)公式为
(4)对于光滑曲面薄片,若由单值函数给出,为曲面在面上的投影区域,则面积为
例求锥面被柱面所截部分的面积
解:图形如下其所截部分在投影为故 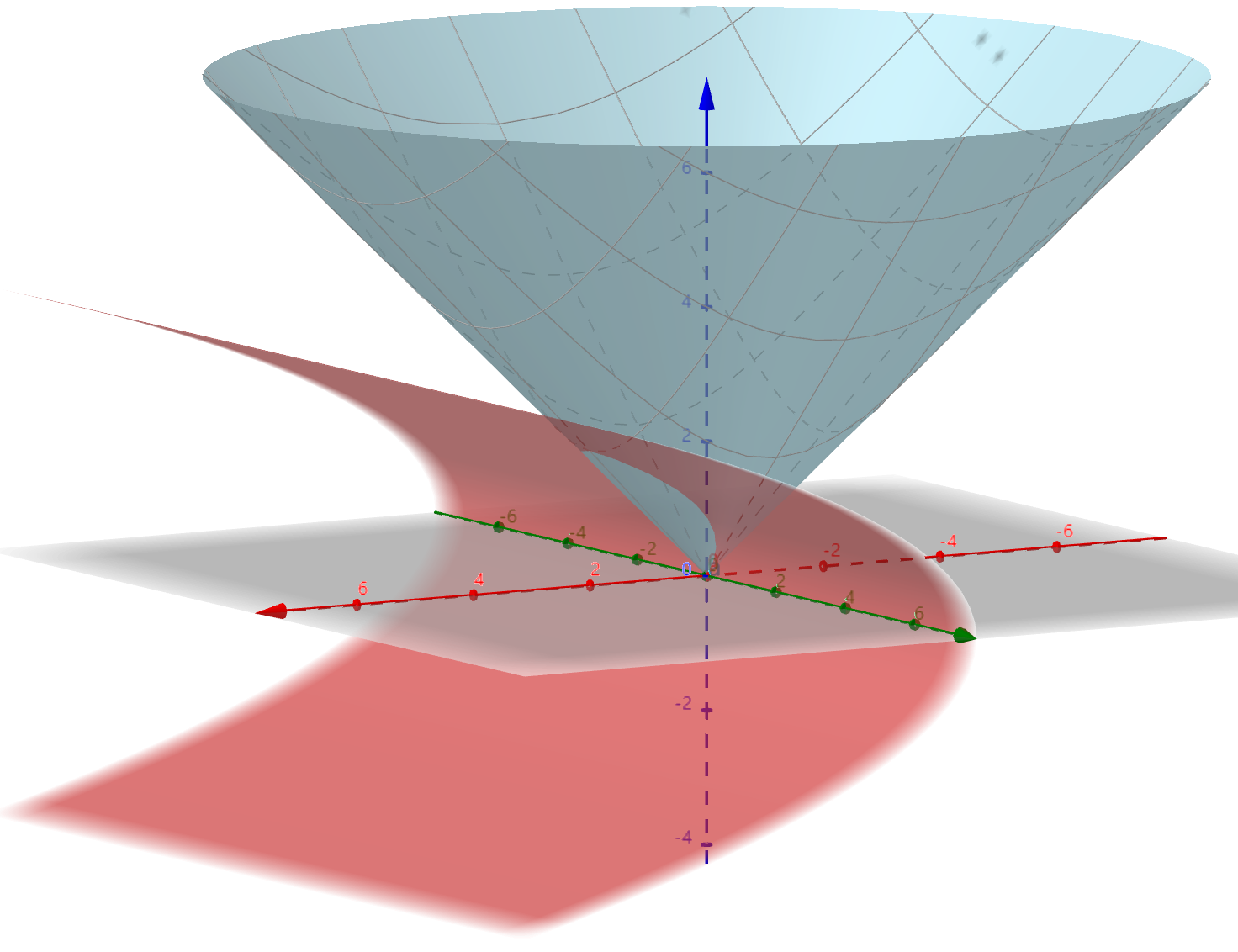
3.2 重心(质心)与形心
以下无特殊说明,均假设与在所定义的区域上连续
(1)对于平面薄片,面密度为,是薄片所占的平面区域,则计算重心的公式为
(2)对于空间物体,体密度为,是物体所占的空间区域,则计算重心公式为
(3)对于光滑曲线,线密度为,则计算重心的公式为
(4)对于光滑曲面薄片,面密度为,则计算重心的公式为
注意:重心就是质心,当密度或者为常数时,重心就成了形心。
补充:
若是一个规则的图形,则容易求得,从而可易于计算
同理:
例设空间物体,求的形心的竖坐标
解:故 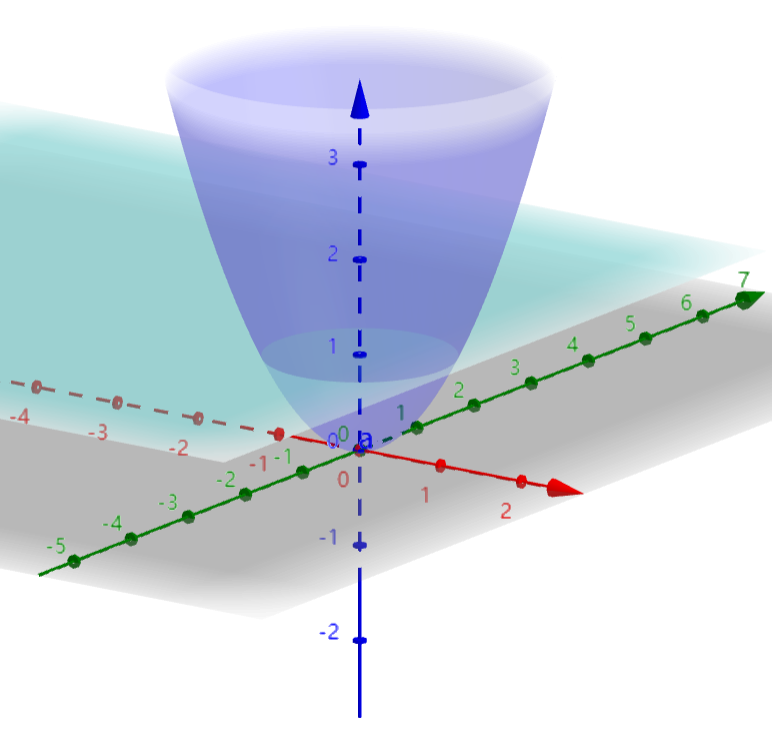
3.3 转动惯量
计算核心是距离
(1)对于平面薄片,面密度为,是薄片所占的平面区域,则计算该薄片对轴、轴和原点的转动惯量公式分别为
(2)对于空间物体,体密度为,是物体所占的空间区域,则计算该物体对轴,轴,轴和原点的转动惯量和公式分别为
(3)对于光滑曲线,线密度为,则计算该曲线对轴,轴,轴和原点的转动量和公式分别为
(4)对于光滑曲面薄片,面密度为,则计算该薄片对轴,轴,轴和原点转动惯量和公式分别为
3.4 引力
(1)对于面上一平面薄片,面密度为,是薄片所占平面区域,则计算该薄片对点处的质量为的质点的引力公式为
其中为引力常量,以下相同
(2)对于空间物体,体密度为,是物体所占的空间区域,则计算该物体对点处的质量为的质点的引力公式为
例由平面图形绕轴旋转所生成的旋转体,其密度,求该旋转体对轴的转动惯量
解:如下图所示旋转体即旋转体为 4. 第二型曲线积分
对坐标的曲线积分指的是:从一点到另一点的一段弧有方向
如果为闭曲线,则对坐标的曲线积分记作
4.1 对坐标曲线积分的性质
性质一:
性质二:设为常数,则
性质三:如果可以分成两段光滑的曲线弧和,即,则
性质四:设是与方向相反的光滑有向弧段,则
该性质是对坐标的曲线积分特有的,因为坐标曲线积分有方向,方向相反则加负号。
2.2 对坐标曲线积分的计算方法
对坐标曲线积分的计算方法同样也是化为定积分后再计算,就曲线弧的方程的不同表示形式,分别进行讨论:
曲线弧的参数方程为:
同时,要求对应的起点,对应的终点,和再上具有一阶连续导数,且则
情况一:
当曲线弧的方程为:,且分别表示为的起点和终点,则
即:谁给谁求导,对应变量直接代入。
情况二:
当曲线弧的方程为:,且分别表示为的起点和终点,则
情况三:
如果为空间曲线弧,且的参数方程为:,分别表示起点和终点则
例计算其中是从点到点的一段有向线段
解:是从点到点线段即为方向向量直线的参数方程为:原式












 ](
](





















