一. 空间向量
1. 空间对称
求对称点方法:关于字母对称,哪个字母不变,其他字母变负。如:
2. 向量的表示
向量表示其中是轴方向的单位向量是轴方向的单位向量是轴方向的单位向量 3. 向量的模和方向余弦
向量的模(大小):就是向量到原点的距离。公式:
向量的单位化:向量的方向不变,模长化为。公式:
方向余弦:向量与坐标轴方向的夹角,有三个,它们分别是与方向的夹角余弦值。公式:
要求:只能在范围内。并且同一方向上
4. 向量的运算
4.1 向量的线性运算
向量的线性运算(加减数乘):设
- ,数乘后的向量和原向量成平行关系与原向量共线
4.2 向量的乘(点乘和叉乘)
例已知求
解:由三角形即共起点向量叉乘的一半可得 5. 向量的投影
在的投影和在的投影
在谁上投影就除以谁的模长在上的投影:在上的投影: 6. 向量的位置关系
位置关系分两种:平行、相交(斜交和垂直)
方法:
- 先看对应坐标是否成比例,如果成比例,则平行
- 如果两个向量点乘等于,则两向量垂直
- 既不平行也不垂直则为斜交,斜交度数:且
二. 平面方程
1. 点法式和一般式
知道平面上的任意一点和法向量就能写出平面方程。法向量
点法式方程:
将上面的点法式方程展开得一般式
判断用点法式还是一般式
条件:若题中已知过原点,平行轴平行面,用一般式方程,其他情况都用点法式方程。
过原点情况下,平行轴(面),平行于哪个字母,哪个字母前系数等于。如:平行,则
过轴:先平行于哪个字母,哪个字母前系数等于再,如:过,则
2. 平面的位置关系
平面的位置关系本质就是它们法向量的位置关系。所以只要找到两个平面的法向量,就能确定它们的位置关系。
注:两平面的夹角范围值
三. 空间直线
1. 空间直线的一般式方程
空间直线可以看作两个空间平面的交线,设两个平面分别为与,则称联立方程组,为空间直线的一般式方程。
空间直线的方向向量为,
2. 空间直线的点向式
把平行于直线的非零向量称为直线的方向向量,并记,设直线过一定点,则直线的点向式方程为:
3. 直线的参数方程
设,其中为参数,则参数方程:
其中前的系数是方向向量。
4. 直线的位置关系
两个直线的位置关系就是他们方向向量的位置关系
注:两直线的夹角范围值
四. 直线与平面的位置关系
直线与平面的位置关系和方向向量与法线的位置关系相差。即:设方向向量和法向量
例求直线和平面的位置关系
解:由题可知方向向量与不成比例不平行于不垂直不垂直于不平行于此时斜交 五. 距离公式
1. 点到点间的距离公式
设点,点
则点到点间的距离公式为:
2 点到平面的距离公式
点到平面的距离公式:
即点代入平面的绝对值平面法向量的模长 例点到平面的距离
解: 3. 两平行平面的距离
平面平面,此时距离公式为:
在计算距离之前要先把和的法向量化为一致。
例两平面平行求两平面距离
解:先将两平面法向量化为一致即两边同除此时法向量 4. 点到空间直线的距离
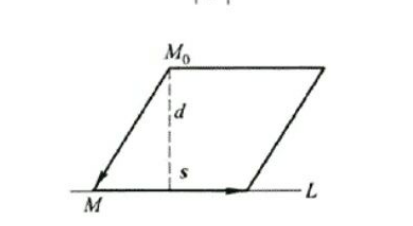
设是直线外一点,是直线上任意一点,且直线的方向向量为,则点到直线的距离:
以上都为取模长
证明:如下图所示,点到直线的距离为,由向量积的几何意义知表示的是以为邻边的平行四边形的面积而距离公式表示以为边长的该平行四边形的高即为点到直线的距离于是 点到空间直线距离证明:
例点到空间直线的距离
解:由题可知平面上的一点方向向量为则 5. 点在平面或直线上的投影
思路:先求出过该点并且和直线平面垂直的平面方程直线方程。之后联立方程求出其交点即可。
例求点在平面的投影点坐标
解:设点过点垂直于平面直线方程为将直线方程化为参数方程将参数方程带入平面方程为从而得坐标点为 例求点在直线上的投影点坐标
解:设点由直线的参数方程可得方向向量由于平面和直线垂直可知方向向量法向量可知平面方程将代入平面方程可得从而投影点坐标为 六. 空间曲面
空间曲面方程特征:
三元全二次:椭球、球面、双曲面、圆锥面三元二次一次:抛物面二元方程:平面或柱面方程两个就是平面一个则为柱面旋转曲面:平方项系数至少有个相同注意:在判断时先把平方项移至等式一边。 柱面在二维中是什么,三位中就是什么柱面。如:在二维中是圆在三维中就是圆柱面
旋转曲面举例:
例是什么空间曲面
解:二维中是两条直线则在三维中是两个平面 七. 旋转曲面求法
旋转曲面一般方程(曲线旋转成面):
这里只研究:坐标平面上的曲线绕坐标轴旋转,上面是上的曲线,其它面一致。
方法:绕谁旋转谁不变,另一变量变成该变量与第三变量平方和的正负平方根。
如:绕轴旋转所得旋转曲面方程:。绕轴旋转所得旋转曲面方程:
求:双曲线绕轴旋转所得旋转曲面 解:绕轴旋转方程绕轴旋转方程 八. 空间曲线
1. 判断空间曲线
空间曲线的一般方程:
曲面曲面 考点:判断空间曲线是什么样的曲线
方法:
- 化简空间曲线的方程组(消元),化简前后方程组中变量个数不变。
- 看化简后的方程组,其中复杂的方程在二维中表示什么曲线,则在三维中就表示什么曲线。
方程组表示的是什么曲线 解:化简两式相减解的代入方程组其中一个此时可以看出方程组中较为复杂方程是一个圆则在三维中也是圆 2. 空间曲线在坐标中的投影
空间曲线关于坐标面投影的柱面方程(二元方程)
- 情况一:母线平行于哪个坐标轴就把对应的变量消去
- 情况二:求关于哪个坐标平面的投影柱面,就把它另外的变量消去
空间曲线在坐标面投影的曲线方程(方程组)
- 方程组中的一个是投影柱面方程(二元方程)
- 方程组中的第二个是坐标面方程。如:投影
求:曲线在平面投影的曲线方程 解:方程为投影柱面方程投影关于平面投影我们消得投影柱面方程可得投影柱面方程由此可得曲线方程 九. 例题
例设向量与共线且求
解:由与共线可知即设且得即 例已知向量与得夹角为且求
解: 例证
解:
